摘要：21．解:(1)依题意.第二年该商品年销售量为万件. 年销售收入为 万元. 则商场该年对该商品征收的总管理费为 故所求函数为 y= 由11.8-p>0及p>0得定义域为0<p<11.8 -----------5分 (2) 由y≥14得≥14 化简得p2-12p+20≤0.即≤0.解得2≤p≤l0 故当比率为[2%.10%]内时.商场收取的管理费将不少于14万元．-8分 (3) 第二年.当商场收取的管理费不少于14万元时. 厂家的销售收入为g(p)= ∵ g(p)= =700(10+)为减函数. ∴ g(p)max =g 故当比率为2%时.厂家销售金额最大.且商场所收管理费又不少于14万元 ---------12分
网址：http://m.1010jiajiao.com/timu3_id_4456090[举报]
如图，
，
，…，
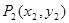，…是曲线
上的点，
，
，…，
，…是
轴正半轴上的点，且
，
，…，
，…
均为斜边在轴上的等腰直角三角形（
为坐标原点）．
（1）写出
、
和
之间的等量关系，以及、和
之间的等量关系；
（2）求证：
（
）；
（3）设
，对所有，
恒成立，求实数
的取值范围．
【解析】第一问利用有
，
得到
第二问证明：①当
时，可求得
，命题成立；②假设当
时，命题成立，即有
则当
时，由归纳假设及
，
得
第三问
．………………………2分
因为函数
在区间
上单调递增，所以当时，
最大为
，即
解：（1）依题意，有，，………………4分
（2）证明：①当时，可求得，命题成立；
……………2分
②假设当时，命题成立，即有，……………………1分
则当时，由归纳假设及，
得．
即
解得
（
不合题意，舍去）
即当时，命题成立． …………………………………………4分
综上所述，对所有，． ……………………………1分
（3） 
．………………………2分
因为函数在区间上单调递增，所以当时，最大为，即
．……………2分
由题意，有
．
所以，
查看习题详情和答案>>