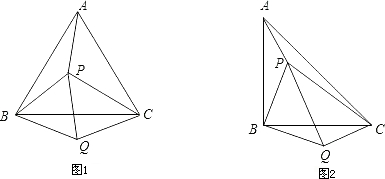
摘要：旋转 例2.如图所示.O是锐角三角形ABC内一点.∠AOB＝ ∠BOC＝∠COA＝120°.P是ΔABC内不同于O的另一点, ΔA1BO1.ΔA1BP1分别由ΔAOB.ΔAPB旋转而得.旋转 角都为60°.则下列结论:①ΔO1BO为等边三角形.且A1.O1.O.C在一条直线上,②A1O1+O1O＝AO+BO,③A1P1+PP1＝PA+PB,④PA+PB+PC>OA+OB+OC.其中正确的有 .
网址：http://m.1010jiajiao.com/timu3_id_445595[举报]
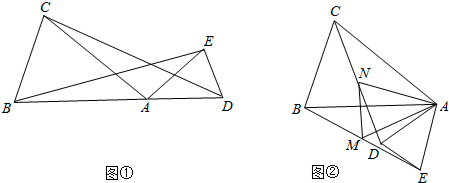
已知，如图①所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B、A、D在一条直线上，连接BE、CD．
（1）求证：BE=CD；
（2）若M、N分别是BE和CD的中点，将△ADE绕点A按顺时针旋转，如图②所示，试证明在旋转过程中，△AMN是等腰三角形；
（3）试证明△AMN与△ABC和△ADE都相似．
查看习题详情和答案>>
（1）求证：BE=CD；
（2）若M、N分别是BE和CD的中点，将△ADE绕点A按顺时针旋转，如图②所示，试证明在旋转过程中，△AMN是等腰三角形；
（3）试证明△AMN与△ABC和△ADE都相似．
如图所示：AB是长为4cm的线段，且CD⊥AB于O，你能借助旋转的方法求出图中阴影部分的面积吗？说说你的做法．
（2013•邵东县模拟）在平面直角坐标系中，如图所示，△AOB是边长为2的等边三角形，将△AOB绕着点B按顺时针方向旋转得到△DCB，使得点D落在x轴的正半轴上，连接OC，AD．（1）求证：OC=AD；
（2）求OC的长；
（3）求过A、D两点的直线的解析式．
如图所示，E是边长为12的正方形ABCD中CD上任意一点，以点A为中心，将△ADE顺时针旋转90°至△ABF的位置，设DE=t