摘要：14．如图四棱锥P-ABCD的底面 是正方形.PB面ABCD.证明:无论四棱锥的高PB怎 样变化.面 PAD与面PCD不可能垂直.
网址：http://m.1010jiajiao.com/timu3_id_4453919[举报]
如图四棱锥P－ABCD的底面是正方形，PD⊥底面ABCD，点E在棱PB上，O为AC与BD的交点．
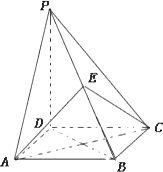
(1)求证：平面
；
(2)当E为PB中点时，求证：OE∥平面PDA，OE∥平面PDC．
(3)当
且E为PB的中点时，求AE与平面PBC所成的角的大小．
如图四棱锥P－ABCD的底面是正方形，PD⊥底面ABCD，点E在棱PB上，O为AC与BD的交点．
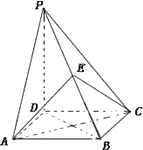
(1)求证：平面AEC⊥平面PDB；
(2)当E为PB中点时，求证：OE∥平面PDA，OE∥平面PDC．
(3)当PD＝
AB且E为PB的中点时，求AE与平面PBC所成的角的大小．
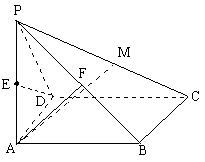如图四棱锥P－ABCD的底面为正方形，PA⊥平面ABCD，AB＝2，PC与平面ABCD成45°角，E、F分别为PA、PB的中点．
（1）求异面直线DE与AF所成角的大小；
（2）设M是PC上的动点，试问当M在何处时，才能使AM⊥平面PBD，证明你的结论．
查看习题详情和答案>>
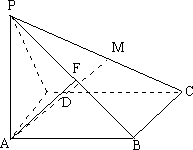
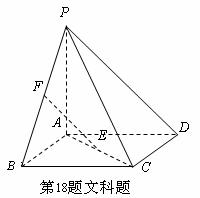(1) 证明: EF∥平面PCD；