摘要:3.第1小题满分6分.第2小题满分10分. 已知四边形为直角梯形.平面.且 (理)若.求:(1)点的坐标, (2)异面直线所成的角. 求证:,(2)求异面直线与所成的角.
网址:http://m.1010jiajiao.com/timu3_id_4453902[举报]
(本题满分16分,第1小题满分4分,第2小题满分6分,第3小题满分6分)
设等比数列 的前
的前 项和为
项和为 ,已知
,已知 .
.
(1)求数列 的通项公式;(2)在
的通项公式;(2)在 与
与 之间插入
之间插入 个1,构成如下的新数列:
个1,构成如下的新数列: ,求这个数列的前
,求这个数列的前 项的和;、(3)在
项的和;、(3)在 与
与 之间插入
之间插入 个数,使这
个数,使这 个数组成公差为
个数组成公差为 的等差数列(如:在
的等差数列(如:在 与
与 之间插入1个数构成第一个等差数列,其公差为
之间插入1个数构成第一个等差数列,其公差为 ;在
;在 与
与 之间插入2个数构成第二个等差数列,其公差为
之间插入2个数构成第二个等差数列,其公差为 ,…以此类推),设第
,…以此类推),设第 个等差数列的和是
个等差数列的和是 . 是否存在一个关于
. 是否存在一个关于 的多项式
的多项式 ,使得
,使得 对任意
对任意 恒成立?若存在,求出这个多项式;若不存在,请说明理由.
恒成立?若存在,求出这个多项式;若不存在,请说明理由.
查看习题详情和答案>>
.(本题满分16分,其中第1小题4分,第2小题6分,第3小题6分,)
如图,已知椭圆 ,
, ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点 为顶点的三角形的周长为
为顶点的三角形的周长为 .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线 和
和 与椭圆的交点分别为
与椭圆的交点分别为 和
和 .
.
(1)求椭圆和双曲线的标准方程;
(2)设直线 、
、 的斜率分别为
的斜率分别为 、
、 ,证明
,证明 ;
;
(3)是否存在常数 ,使得
,使得
恒成立?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看习题详情和答案>>
(本题满分16分,第1小题满分4分,第2小题满分6分,第3小题满分6分)
设等比数列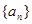 的前
的前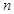 项和为
项和为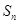 ,已知
,已知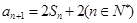 .
.
(1)求数列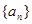 的通项公式;(2)在
的通项公式;(2)在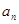 与
与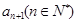 之间插入
之间插入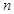 个1,构成如下的新数列:
个1,构成如下的新数列: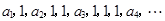 ,求这个数列的前
,求这个数列的前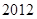 项的和;、(3)在
项的和;、(3)在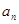 与
与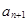 之间插入
之间插入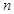 个数,使这
个数,使这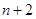 个数组成公差为
个数组成公差为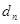 的等差数列(如:在
的等差数列(如:在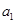 与
与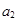 之间插入1个数构成第一个等差数列,其公差为
之间插入1个数构成第一个等差数列,其公差为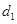 ;在
;在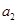 与
与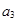 之间插入2个数构成第二个等差数列,其公差为
之间插入2个数构成第二个等差数列,其公差为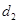 ,…以此类推),设第
,…以此类推),设第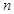 个等差数列的和是
个等差数列的和是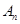 . 是否存在一个关于
. 是否存在一个关于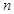 的多项式
的多项式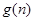 ,使得
,使得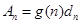 对任意
对任意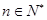 恒成立?若存在,求出这个多项式;若不存在,请说明理由.
恒成立?若存在,求出这个多项式;若不存在,请说明理由.
设等比数列
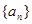 的前
的前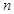 项和为
项和为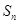 ,已知
,已知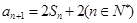 .
.(1)求数列
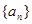 的通项公式;(2)在
的通项公式;(2)在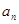 与
与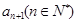 之间插入
之间插入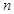 个1,构成如下的新数列:
个1,构成如下的新数列: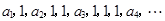 ,求这个数列的前
,求这个数列的前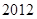 项的和;、(3)在
项的和;、(3)在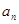 与
与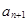 之间插入
之间插入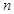 个数,使这
个数,使这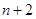 个数组成公差为
个数组成公差为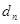 的等差数列(如:在
的等差数列(如:在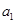 与
与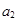 之间插入1个数构成第一个等差数列,其公差为
之间插入1个数构成第一个等差数列,其公差为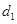 ;在
;在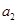 与
与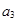 之间插入2个数构成第二个等差数列,其公差为
之间插入2个数构成第二个等差数列,其公差为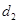 ,…以此类推),设第
,…以此类推),设第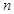 个等差数列的和是
个等差数列的和是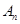 . 是否存在一个关于
. 是否存在一个关于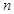 的多项式
的多项式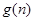 ,使得
,使得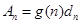 对任意
对任意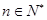 恒成立?若存在,求出这个多项式;若不存在,请说明理由.
恒成立?若存在,求出这个多项式;若不存在,请说明理由.