摘要: 一条直线l过定点P(1,2), 且与 点M距离相等, 则l的方程是
网址:http://m.1010jiajiao.com/timu3_id_4452710[举报]
动圆C过定点F(
,0),且与直线x=-
相切,其中p>0.设圆心C的轨迹Γ的程为F(x,y)=0
(1)求F(x,y)=0;
(2)曲线Γ上的一定点P(x0,y0)(y0≠0),方向向量
=(y0,-p)的直线l(不过P点)与曲线Γ交与A、B两点,设直线PA、PB斜率分别为kPA,kPB,计算kPA+kPB;
(3)曲线Γ上的两个定点P0(x0,y0)、Q0(x0′,y0′),分别过点P0,Q0作倾斜角互补的两条直线P0M,Q0N分别与曲线Γ交于M,N两点,求证直线MN的斜率为定值.
查看习题详情和答案>>
| p |
| 2 |
| p |
| 2 |
(1)求F(x,y)=0;
(2)曲线Γ上的一定点P(x0,y0)(y0≠0),方向向量
| d |
(3)曲线Γ上的两个定点P0(x0,y0)、Q0(x0′,y0′),分别过点P0,Q0作倾斜角互补的两条直线P0M,Q0N分别与曲线Γ交于M,N两点,求证直线MN的斜率为定值.
已知点P为圆 x2+y2=4上的动点,且P不在x 轴上,PD⊥x 轴,垂足为D,线段PD中点Q的轨迹为曲线C,过定点M(t,0)(0< t <2)任作一条与y轴不垂直的直线l ,它与曲线C交于A、B两点。
(1)求曲线C的方程;
(2)试证明:在x轴上存在定点N,使得∠ANB总能被x轴平分
查看习题详情和答案>>
(1)求曲线C的方程;
(2)试证明:在x轴上存在定点N,使得∠ANB总能被x轴平分
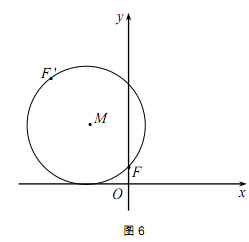
如图6,已知动圆M过定点F(1,0)且与x轴相切,点F 关于圆心M 的对称点为 F',动点F’的轨迹为C.
(1)求曲线C的方程;
(2)设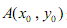 是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P
、Q.
是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P
、Q.
①证明:直线PQ的斜率为定值;
②记曲线C位于P 、Q两点之间的那一段为l.若点B在l上,且点B到直线PQ的
距离最大,求点B的坐标.
查看习题详情和答案>>
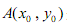 是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P 、Q.
是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P 、Q.