摘要:问题背景 某课外学习小组在一次学习研讨中.得到了如下两个命题: ①如图1.在正三角形△ABC中.M.N分别是AC.AB上的点.BM与CN相交于点O.若∠BON=60º.则BM=CN, ②如图2.在正方形ABCD中.M.N分别是CD.AD上的点.BM与CN相交于点O.若∠BON=90º.则BM=CN, 然后运用类比的思想提出了如下命题: ③如图3.在正五边形ABCDE中.M.N分别是CD.DE上的点.BM与CN相交于点O.若∠BON=108º.则BM=CN. 任务要求: (1)请你从①.②.③三个命题中选择一个进行证明,(说明:选①做对得4分.选②做对得3分.选③做对得5分) (2)请你继续完成下列探索: ①请在图3中画出一条与CN相等的线段DH.使点H在正五边形的边上.且与CN相交所成的一个角是108º.这样的线段有几条?(不必写出画法.不要求证明) ②如图4.在正五边形ABCDE中.M.N分别是DE.EA上的点.BM与CN相交于点O.若∠BON=108º.请问结论BM=CN是否还成立?若成立.请给予证明,若不成立.请说明理由. [解] (1)以下答案供参考: (1) 如选命题① 证明:在图1中.∵∠BON=60°∴∠1+∠2=60° ∵∠3+∠2=60°.∴∠1=∠3 又∵BC=CA.∠BCM=∠CAN=60°∴ΔBCM≌ΔCAN ∴BM=CN (2)如选命题② 证明:在图2中.∵∵∠BON=90°∴∠1+∠2=90° ∵∠3+∠2=90°.∴∠1=∠3 又∵BC=CD.∠BCM=∠CDN=90°∴ΔBCM≌ΔCDN ∴BM=CN (3)如选命题③ 证明,在图3中.∵∠BON=108°∴∠1+∠2=108° ∵∠2+∠3=108°∴∠1=∠3 又∵BC=CD.∠BCM=∠CDN=108° ∴ΔBCM≌ΔCDN ∴BM=CN (2)①答:当∠BON=时结论BM=CN成立. ②答当∠BON=108°时.BM=CN还成立 证明,如图5连结BD.CE. 在△BCI)和△CDE中 ∵BC=CD, ∠BCD=∠CDE=108°,CD=DE ∴ΔBCD≌ ΔCDE ∴BD=CE , ∠BDC=∠CED, ∠DBC=∠CEN ∵∠CDE=∠DEC=108°, ∴∠BDM=∠CEN ∵∠OBC+∠ECD=108°, ∠OCB+∠OCD=108° ∴∠MBC=∠NCD 又∵∠DBC=∠ECD=36°, ∴∠DBM=∠ECN ∴ΔBDM≌ ΔCNE ∴BM=CN
网址:http://m.1010jiajiao.com/timu3_id_444978[举报]
(2006•江西)问题背景:某课外学习小组在一次学习研讨中,得到了如下两个命题:
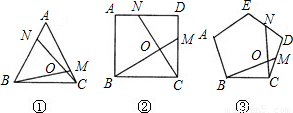
①如图1,在正三角形ABC中,M,N分别是AC,AB上的点,BM与CN相交于点O,若∠BON=60°,则BM=CN;
②如图2,在正方形ABCD中,M,N分别是CD,AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.
然后运用类比的思想提出了如下命题;
③如图3,在正五边形ABCDE中,M,N分别是CD,DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.任务要求:
(1)请你从①,②,③三个命题中选择一个进行证明;
(2)请你继续完成下面的探索:
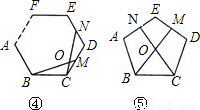
①如图4,在正n(n≥3)边形ABCDEF…中,M,N分别是CD,DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立;(不要求证明)
②如图5,在正五边形ABCDE中,M,N分别是DE,AE上的点,BM与CN相交于点O,若∠BON=108°时,试问结论BM=CN是否还成立.若成立,请给予证明;若不成立,请说明理由.
查看习题详情和答案>>


①如图1,在正三角形ABC中,M,N分别是AC,AB上的点,BM与CN相交于点O,若∠BON=60°,则BM=CN;
②如图2,在正方形ABCD中,M,N分别是CD,AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.
然后运用类比的思想提出了如下命题;
③如图3,在正五边形ABCDE中,M,N分别是CD,DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.任务要求:
(1)请你从①,②,③三个命题中选择一个进行证明;
(2)请你继续完成下面的探索:
①如图4,在正n(n≥3)边形ABCDEF…中,M,N分别是CD,DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立;(不要求证明)
②如图5,在正五边形ABCDE中,M,N分别是DE,AE上的点,BM与CN相交于点O,若∠BON=108°时,试问结论BM=CN是否还成立.若成立,请给予证明;若不成立,请说明理由.
查看习题详情和答案>>
(2006•江西)问题背景:某课外学习小组在一次学习研讨中,得到了如下两个命题:
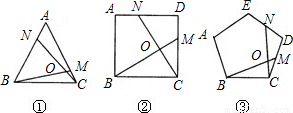
①如图1,在正三角形ABC中,M,N分别是AC,AB上的点,BM与CN相交于点O,若∠BON=60°,则BM=CN;
②如图2,在正方形ABCD中,M,N分别是CD,AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.
然后运用类比的思想提出了如下命题;
③如图3,在正五边形ABCDE中,M,N分别是CD,DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.任务要求:
(1)请你从①,②,③三个命题中选择一个进行证明;
(2)请你继续完成下面的探索:
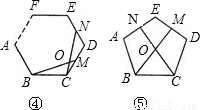
①如图4,在正n(n≥3)边形ABCDEF…中,M,N分别是CD,DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立;(不要求证明)
②如图5,在正五边形ABCDE中,M,N分别是DE,AE上的点,BM与CN相交于点O,若∠BON=108°时,试问结论BM=CN是否还成立.若成立,请给予证明;若不成立,请说明理由.
查看习题详情和答案>>


①如图1,在正三角形ABC中,M,N分别是AC,AB上的点,BM与CN相交于点O,若∠BON=60°,则BM=CN;
②如图2,在正方形ABCD中,M,N分别是CD,AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.
然后运用类比的思想提出了如下命题;
③如图3,在正五边形ABCDE中,M,N分别是CD,DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.任务要求:
(1)请你从①,②,③三个命题中选择一个进行证明;
(2)请你继续完成下面的探索:
①如图4,在正n(n≥3)边形ABCDEF…中,M,N分别是CD,DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立;(不要求证明)
②如图5,在正五边形ABCDE中,M,N分别是DE,AE上的点,BM与CN相交于点O,若∠BON=108°时,试问结论BM=CN是否还成立.若成立,请给予证明;若不成立,请说明理由.
查看习题详情和答案>>
(2006•江西)问题背景:某课外学习小组在一次学习研讨中,得到了如下两个命题:
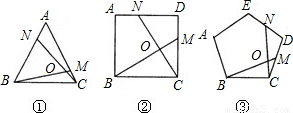
①如图1,在正三角形ABC中,M,N分别是AC,AB上的点,BM与CN相交于点O,若∠BON=60°,则BM=CN;
②如图2,在正方形ABCD中,M,N分别是CD,AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.
然后运用类比的思想提出了如下命题;
③如图3,在正五边形ABCDE中,M,N分别是CD,DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.任务要求:
(1)请你从①,②,③三个命题中选择一个进行证明;
(2)请你继续完成下面的探索:
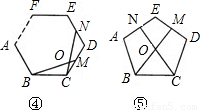
①如图4,在正n(n≥3)边形ABCDEF…中,M,N分别是CD,DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立;(不要求证明)
②如图5,在正五边形ABCDE中,M,N分别是DE,AE上的点,BM与CN相交于点O,若∠BON=108°时,试问结论BM=CN是否还成立.若成立,请给予证明;若不成立,请说明理由.
查看习题详情和答案>>


①如图1,在正三角形ABC中,M,N分别是AC,AB上的点,BM与CN相交于点O,若∠BON=60°,则BM=CN;
②如图2,在正方形ABCD中,M,N分别是CD,AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.
然后运用类比的思想提出了如下命题;
③如图3,在正五边形ABCDE中,M,N分别是CD,DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.任务要求:
(1)请你从①,②,③三个命题中选择一个进行证明;
(2)请你继续完成下面的探索:
①如图4,在正n(n≥3)边形ABCDEF…中,M,N分别是CD,DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立;(不要求证明)
②如图5,在正五边形ABCDE中,M,N分别是DE,AE上的点,BM与CN相交于点O,若∠BON=108°时,试问结论BM=CN是否还成立.若成立,请给予证明;若不成立,请说明理由.
查看习题详情和答案>>
(2006•江西)问题背景:某课外学习小组在一次学习研讨中,得到了如下两个命题:
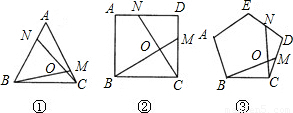

①如图1,在正三角形ABC中,M,N分别是AC,AB上的点,BM与CN相交于点O,若∠BON=60°,则BM=CN;
②如图2,在正方形ABCD中,M,N分别是CD,AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.
然后运用类比的思想提出了如下命题;
③如图3,在正五边形ABCDE中,M,N分别是CD,DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.任务要求:
(1)请你从①,②,③三个命题中选择一个进行证明;
(2)请你继续完成下面的探索:
①如图4,在正n(n≥3)边形ABCDEF…中,M,N分别是CD,DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立;(不要求证明)
②如图5,在正五边形ABCDE中,M,N分别是DE,AE上的点,BM与CN相交于点O,若∠BON=108°时,试问结论BM=CN是否还成立.若成立,请给予证明;若不成立,请说明理由.
查看习题详情和答案>>


①如图1,在正三角形ABC中,M,N分别是AC,AB上的点,BM与CN相交于点O,若∠BON=60°,则BM=CN;
②如图2,在正方形ABCD中,M,N分别是CD,AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.
然后运用类比的思想提出了如下命题;
③如图3,在正五边形ABCDE中,M,N分别是CD,DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.任务要求:
(1)请你从①,②,③三个命题中选择一个进行证明;
(2)请你继续完成下面的探索:
①如图4,在正n(n≥3)边形ABCDEF…中,M,N分别是CD,DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立;(不要求证明)
②如图5,在正五边形ABCDE中,M,N分别是DE,AE上的点,BM与CN相交于点O,若∠BON=108°时,试问结论BM=CN是否还成立.若成立,请给予证明;若不成立,请说明理由.
查看习题详情和答案>>