摘要: 解:(1)过点B作BQ⊥OA于点Q. ∵ 点A坐标是. ∴点A1坐标为(-10+m.-3).OA=10. -------2分 又∵ 点B坐标是. ∴BQ=6.OQ=8. 在Rt△OQB中. -3分 ∴OA=OB=10.. 由翻折的性质可知.PA=OA=10.PB=OB=10. ∴四边形OAPB是菱形. ∴PB∥AO.∴P点坐标为. -----5分 ∴P1点坐标为(-18+m.3). ------6分 (2)①当0<m≤4时., 过点B1作B1Q1⊥x轴于点Q1.则B1 Q1=6-3=3.设O1B1 交x轴于点F.∵O1B1∥BO.∴∠α=∠β. 在Rt△FQ1B1中.. ∴.∴Q1F=4. ∴B1F==5. ∵AQ=OA-OQ=10-8=2. ∴AF=AQ+QQ1+ Q1F=2+m+4=6+m. ∴面积s=3AF =2m+12--9分 ②当4<m<14时. 设P1A1交x轴于点S.P1B1交OB 于点H. 由平移性质.得 OH=B1F=5. 此时AS=m-4. ∴OS=OA-AS =10-(m-4)=14-m. ∴面积s=3OS=3(5+14-m)=-3 m+57. --12分
网址:http://m.1010jiajiao.com/timu3_id_444893[举报]
画∠AOB=60°,画∠AOB的平分线OC,在OC上取一点D,使OD=4cm,过点D作边OA的平行线DE,过点D作OB的垂线DF,垂足为F,测量点D到OB的距离.(精确到0.1cm)
查看习题详情和答案>>
 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOC=60°,点A在第一象限,过点A的双曲线为y=
如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOC=60°,点A在第一象限,过点A的双曲线为y=| k |
| x |
(1)当点O′与点A重合时,t的值是
4
4
;(2)当B′落在双曲线上时,t的值是
2
| 5 |
2
.| 5 |
如图,四边形OABC是等腰梯形,OA∥BC,A的坐标(4,0),B的坐标(3,2),点M从O点以每秒3个单位的速度向终点A运动;同时点N从B点出发以每秒1个单位的速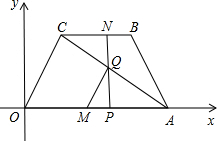 度向终点C运动(M到达点A后停止,点N继续运动到C点停止),过点N作NP⊥OA于P点,连接AC交NP于Q,连接MQ,如动点N运动时间为t秒.
度向终点C运动(M到达点A后停止,点N继续运动到C点停止),过点N作NP⊥OA于P点,连接AC交NP于Q,连接MQ,如动点N运动时间为t秒.
(1)求直线AC的解析式;
(2)当t取何值时?△AMQ的面积最大,并求此时△AMQ面积的最大值;
(3)是否存在t的值,使△PQM与△PQA相似?若存在,求出t的值;若不存在,请说明理由. 查看习题详情和答案>>
 度向终点C运动(M到达点A后停止,点N继续运动到C点停止),过点N作NP⊥OA于P点,连接AC交NP于Q,连接MQ,如动点N运动时间为t秒.
度向终点C运动(M到达点A后停止,点N继续运动到C点停止),过点N作NP⊥OA于P点,连接AC交NP于Q,连接MQ,如动点N运动时间为t秒.(1)求直线AC的解析式;
(2)当t取何值时?△AMQ的面积最大,并求此时△AMQ面积的最大值;
(3)是否存在t的值,使△PQM与△PQA相似?若存在,求出t的值;若不存在,请说明理由. 查看习题详情和答案>>
如图,在平面直角坐标系xOy中,抛物线y=
x2-
x-10与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连接AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒).
(1)求A,B,C三点的坐标和抛物线的顶点的坐标;
(2)当t为何值时,四边形PQCA为平行四边形?请写出计算过程;
(3)当0<t<
时,△PQF的面积是否总为定值?若是,求出此定值, 若不是,请说明理由;
若不是,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?请写出解答过程. 查看习题详情和答案>>
| 1 |
| 18 |
| 4 |
| 9 |
(1)求A,B,C三点的坐标和抛物线的顶点的坐标;
(2)当t为何值时,四边形PQCA为平行四边形?请写出计算过程;
(3)当0<t<
| 9 |
| 2 |
 若不是,请说明理由;
若不是,请说明理由;(4)当t为何值时,△PQF为等腰三角形?请写出解答过程. 查看习题详情和答案>>
 如图,点P是∠AOB的角平分线上一点,过点P作PC∥OA交OB于点C.若∠AOB=60°,OC=4,则点P到OA的距离PD等于
如图,点P是∠AOB的角平分线上一点,过点P作PC∥OA交OB于点C.若∠AOB=60°,OC=4,则点P到OA的距离PD等于