摘要:用数来解决形的问题.如图,边长为1的正方形方格纸上,有A.B.C.D 四点. (1)求证:△ADC ∽ △BDA (2)求∠B+∠D度数.
网址:http://m.1010jiajiao.com/timu3_id_444881[举报]
问题提出:
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小. 而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形. 并利用差的符号来确定它们的大小,即耍比较代数式 M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0;则 M<N.
问题解决:
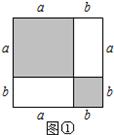
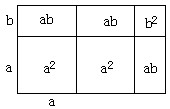
如图①.把边长为 a+b(a≠b)的大正方形分割成两个边长分别是 a、b 的小正方形及两个矩形,试比较两个小正方形的面积之和 M与两个矩形面积之和N 的大小.类比应用:
(1)已知小丽和小颖购买同一种商品的平均价格分别为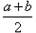 元/千克、
元/千克、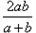 元/千克(a·b是正数.且a≠b),试比较小丽和小颖所购商品的平均价格的高低.
元/千克(a·b是正数.且a≠b),试比较小丽和小颖所购商品的平均价格的高低.
(2)试比技图②、图③两个矩形的周长 M, 、N, 的大小(b>c).
图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形
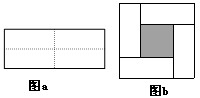
(1)你认为图b中的阴影部分的正方形的边长等于多少( );
(2)请用两种不同的方法求图b中阴影部分的面积。方法1:( ),方法2:( );
(3)观察图b你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2,(m-n)2,mn:( )。
(4)根据(3)题中的等量关系,解决如下问题:若a+b=7,ab=5,则(a-b)2=( )。我们已经知道,完全平方公式可以用平面几何图形的面积来表示,实际上还有一些代数等式也可以用这种形式表示,请写出图中所表示的代数恒等式( )。
(2)请用两种不同的方法求图b中阴影部分的面积。方法1:( ),方法2:( );
(3)观察图b你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2,(m-n)2,mn:( )。
(4)根据(3)题中的等量关系,解决如下问题:若a+b=7,ab=5,则(a-b)2=( )。我们已经知道,完全平方公式可以用平面几何图形的面积来表示,实际上还有一些代数等式也可以用这种形式表示,请写出图中所表示的代数恒等式( )。
 ,PC=1.求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1.求∠BPC度数的大小和等边三角形ABC的边长. .问题得到解决.?
.问题得到解决.? ,BP=
,BP= ,PC=1.求∠BPC度数的大小和正方形ABCD的边长.
,PC=1.求∠BPC度数的大小和正方形ABCD的边长.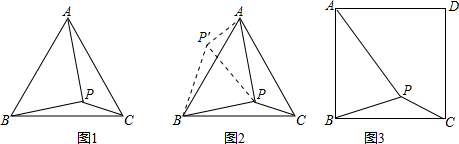
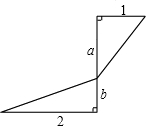 式子
式子 可以理解为“以a、b为直角边长的直角三角形的斜边长”,利用这个知识,我们可以恰当地构造图形来解决一些数学问题.比如在解“已知a+b=2,则
可以理解为“以a、b为直角边长的直角三角形的斜边长”,利用这个知识,我们可以恰当地构造图形来解决一些数学问题.比如在解“已知a+b=2,则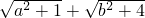 的最小值为________”时,我们就可以构造两个直角三角形,转化为“求两个直角三角形的斜边和最小是多少”的问题.请你根据所给图形和题意,在横线上填上正确的答案.
的最小值为________”时,我们就可以构造两个直角三角形,转化为“求两个直角三角形的斜边和最小是多少”的问题.请你根据所给图形和题意,在横线上填上正确的答案.