摘要： 直线l∥m,A.B为l上两定点,CD为直线m上的两点,且CD=AB,当线段C.D在直线m上左.右移动时,凸四边形ABCD的面积. [ ] A.变大 B.变小 C.不变 D.不能确定
网址：http://m.1010jiajiao.com/timu3_id_443722[举报]
已知:直线
与直线
平行,且它们之间的距离为2,A，B是直线上的两个定
点，C，D是直线上的两个动点(点C在点D的左侧)，AB=CD=5，连接AC、BD、BC，
将△ABC沿BC折叠得到△A1BC.
（1）求四边形ABDC的面积；
（2）当A1与D重合时，四边形ABDC是什么特殊四边形，为什么？
（3）当A1与D不重合时
①连接A1 D，求证：A1 D∥BC;
②若以A1，B，C，D为顶点的四边形为矩形，且矩形的边长分别为
，
，
求（+）2的值.
 |
查看习题详情和答案>>
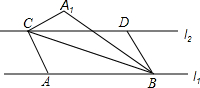已知：直线l1与直线l2平行，且它们之间的距离为2，A、B是直线l1上的两个定点，C、D是直线l2上的两个动点（点C在点D的左侧），AB=CD=5，连接AC、BD、BC，将△ABC沿BC折叠得到△A1BC．（1）求四边形ABDC的面积．
（2）当A1与D重合时，四边形ABDC是什么特殊四边形，为什么？
（3）当A1与D不重合时
①连接A1、D，求证：A1D∥BC；
②若以A1，B，C，D为顶点的四边形为矩形，且矩形的边长分别为a，b，求（a+b）2的值．
如图，直线y=-
x+3分别交x轴、y轴于A、B两点，线段OA上有一动点P由原点O向点A运动，速度为每秒1个单位长度，设运动时间为t秒．
（1）直接填出两点的坐标：A：______，B：______；
（2）过点P作直线截△ABO，使截得的三角形与△ABO相似，若当P在某一位置时，满足条件的直线共有4条，t的取值范围是______；
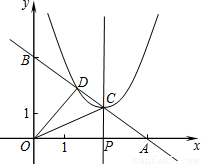
（3）如图，过点P作x轴的垂线交直线AB于点C，设以C为顶点的抛物线 y=（x+m）2+n与直线AB的另一交点为D，
①用含t的代数式分别表示m=______，n=______；
②随着点P运动，CD的长是否为定值？若是，请求出CD长；若不是，说明理由；
③设△COD的OC边上的高为h，请直接写出当t为何值时，h的值最大？
查看习题详情和答案>>
x+3分别交x轴、y轴于A、B两点，线段OA上有一动点P由原点O向点A运动，速度为每秒1个单位长度，设运动时间为t秒．（1）直接填出两点的坐标：A：______，B：______；
（2）过点P作直线截△ABO，使截得的三角形与△ABO相似，若当P在某一位置时，满足条件的直线共有4条，t的取值范围是______；
（3）如图，过点P作x轴的垂线交直线AB于点C，设以C为顶点的抛物线 y=（x+m）2+n与直线AB的另一交点为D，
①用含t的代数式分别表示m=______，n=______；
②随着点P运动，CD的长是否为定值？若是，请求出CD长；若不是，说明理由；
③设△COD的OC边上的高为h，请直接写出当t为何值时，h的值最大？
查看习题详情和答案>>
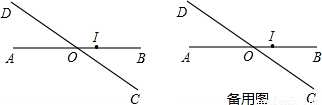
平面上有两条直线AB、CD相交于点O，且∠BOD=150°（如图），现按如下要求规定此平面上点的“距离坐标”：
（1）点O的“距离坐标”为（0，0）；
（2）在直线CD上，且到直线AB的距离为p（p＞0）的点的“距离坐标”为（p，0）；在直线AB上，且到直线CD的距离为q（q＞0）的点的“距离坐标”为（0，q）；
（3）到直线AB、CD的距离分别为p，q（p＞0，q＞0）的点的“距离坐标”为（p，q）．
设M为此平面上的点，其“距离坐标”为（m，n），根据上述对点的“距离坐标”的规定，解决下列问题：
（1）画出图形（保留画图痕迹）：
①满足m=1，且n=0的点M的集合；
②满足m=n的点M的集合；
（2）若点M在过点O且与直线CD垂直的直线l上，求m与n所满足的关系式．（说明：图中OI长为一个单位长）
查看习题详情和答案>>
（1）点O的“距离坐标”为（0，0）；
（2）在直线CD上，且到直线AB的距离为p（p＞0）的点的“距离坐标”为（p，0）；在直线AB上，且到直线CD的距离为q（q＞0）的点的“距离坐标”为（0，q）；
（3）到直线AB、CD的距离分别为p，q（p＞0，q＞0）的点的“距离坐标”为（p，q）．
设M为此平面上的点，其“距离坐标”为（m，n），根据上述对点的“距离坐标”的规定，解决下列问题：
（1）画出图形（保留画图痕迹）：
①满足m=1，且n=0的点M的集合；
②满足m=n的点M的集合；
（2）若点M在过点O且与直线CD垂直的直线l上，求m与n所满足的关系式．（说明：图中OI长为一个单位长）
查看习题详情和答案>>