摘要：15．∠A和∠C是矩形ABCD的一组对角.则①∠ A与∠C相等,②∠A与∠C互补,③∠A是直角,④∠C是直角.以上结论中.正确的有 ( ) A 1个 B 2个 C 3个 D 4个

网址：http://m.1010jiajiao.com/timu3_id_443567[举报]

17、∠A和∠C是矩形ABCD的一组对角，则①∠A与∠C相等；②∠A与∠C互补；③∠A是直角；④∠C是直角．以上结论中，正确的有（　　）

查看习题详情和答案>>

∠A和∠C是矩形ABCD的一组对角，则①∠A与∠C相等；②∠A与∠C互补；③∠A是直角；④∠C是直角．以上结论中，正确的有

A.
1个
B.
2个
C.
3个
D.
4个

查看习题详情和答案>>

如图，四边形ABCD是正方形，P是对角线BD上一点，过P点作直线MN和EF，分别平行于AB、BC，交两组对边于点M、N、E、F，则四边形PFDN、PEBM都是正方形，四边形PEAN、PMCF都是矩形，设正方形PEBM的边长为a，正方形PFDN

的边长为b（a＜b）．
（1）用代数式分别表示正方形PEBM和正方形PFDN的面积之和以及矩形PEAN与矩形PMCF的面积之和，并判定两个面积之和的大小．
（2）当点P在什么位置时，它们的面积之和相等？
（3）用含a、b的代数式表示S_△EMD．查看习题详情和答案>>

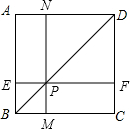如图，四边形ABCD是正方形，P是对角线BD上一点，过P点作直线MN和EF，分别平行于AB、BC，交两组对边于点M、N、E、F，则四边形PFDN、PEBM都是正方形，四边形PEAN、PMCF都是矩形，设正方形PEBM的边长为a，正方形PFDN的边长为b（a＜b）．
（1）用代数式分别表示正方形PEBM和正方形PFDN的面积之和以及矩形PEAN与矩形PMCF的面积之和，并判定两个面积之和的大小．
（2）当点P在什么位置时，它们的面积之和相等？
（3）用含a、b的代数式表示S_△EMD．

查看习题详情和答案>>

八年级数学学习合作小组在学过《图形的相似》这一章后，发现可将相似三角形的定义、判定以及性质拓展到矩形、菱形的相似中去．如：我们可以定义：“长和宽之比相等的矩形是相似矩形．”相似矩形也有以下的性质：相似矩形的对角线之比等于相似比，周长比等于相似比，面积比等于相似比的平方等等．请你参与这个学习小组，一同探索这类问题：
（1）写出判定菱形相似的一种判定方法：若有一组角对应相等（或两组对角线对应成比例），则这两个菱形相似；
（2）如图，将菱形ABCD沿着直线AC向右平移后得到菱形A′B′C′D′，试证明：四边形A′FCE是菱形，且菱形ABCD∽菱形A′FCE；
（3）若AC=

，菱形A′FCE的面积是菱形ABCD面积的一半，求平移的距离AA′的长．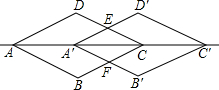

查看习题详情和答案>>