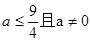摘要： 已知抛物线y＝x2-2x+m与x轴交于点A(x1.0).B(x2.0)(x2＞x1). 在抛物线y＝x2-2x+m上.求m的值, (2)若抛物线y＝ax2+bx+m与抛物线y＝x2-2x+m关于y轴对称.点Q1(-2.q1).Q2(-3.q2)都在抛物线y＝ax2+bx+m上.则q1.q2的大小关系是 (请将结论写在横线上.不要写解答过程), (友情提示:结论要填在答题卡相应的位置上) (3)设抛物线y＝x2-2x+m的顶点为M.若△AMB是直角三角形.求m的值.
网址：http://m.1010jiajiao.com/timu3_id_442355[举报]
已知抛物线y＝－x2＋2mxm2m＋2．
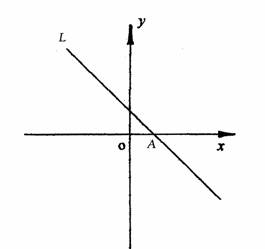
（1）判断抛物线的顶点与直线L：y＝-x＋2的位置关系；
（2）设该抛物线与x轴交于M、N两点，当OM?ON＝4，且OM≠ON时，求出这条抛物线的解析式；
（3）直线L交x轴于点A，（2）中所求抛物线的对称轴与x轴交于点B．那么在对称轴上是否存在点P，使⊙P与直线L和x轴同时相切．若存在，求出点P的坐标；若不存在，请说明理由．
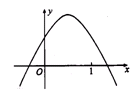
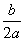＞0．其中正确的结论有( ) 
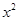－3x+1与x轴有交点，则a的取值范围是（ ）
B、
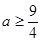D、
