摘要： 如图.抛物线y=―x2+(6―)x+m―3与x轴交于A(x1.0).B(x2.0)两点(x1＜x2).交y轴于C点.且x1+x2=0. (1)求抛物线的解析式.并写出顶点坐标及对称轴方程. (2)在抛物线上是否存在一点P使△PBC≌△OBC. 若存在.求出点P的坐标.若不存在.请说明理由.
网址：http://m.1010jiajiao.com/timu3_id_440804[举报]
如图，抛物线y=x2+bx+c与x轴交于A、B两点，与y轴交于点C，∠OBC=45，则下列各式成立的是 ( )
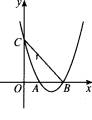
A．b-c-1=0
B．b+c-1=0
C．b-c+1=0
D．b+c-1=0
查看习题详情和答案>>
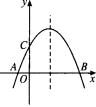
如图，抛物线的对称轴是直线x=1，它与x轴交于A、B两点，与y轴
交于C点．点A、C的坐标分别是(-1，0)、(0，
)．
(1)求此抛物线对应的函数解析式；
(2)若点P是抛物线上位于x轴上方的一个动点，求△ABP面积的最大值．
查看习题详情和答案>>
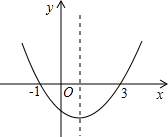列说法正确的是（ ）
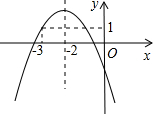如图，抛物线y=ax2+bx+c过点（-3，1）对称轴为直线x=-2，下列结论错误的是（ ）
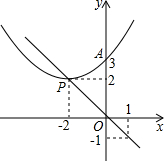（2013•河南模拟）如图，抛物线y=ax2+bx+c的顶点为P（-2，2），且与y轴交于点A（0，3）．若平移该抛物线使其顶点P沿直线y=-x由（-2，2）移动到（1，-1），此时抛物线与y轴交于点A′，则AA′的长度为（ ）