摘要:已知:在平面直角坐标系xOy中.一次函数的图象与x轴交于点A.抛物线经过O.A两点. (1)试用含a的代数式表示b, (2)设抛物线的顶点为D.以D为圆心.DA为半径的圆被x轴分为劣弧和优弧两部分.若将劣弧沿x轴翻折.翻折后的劣弧落在⊙D内.它所在的圆恰与OD相切.求⊙D半径的长及抛物线的解析式, 中条件的优弧上的一个动点.抛物线在x轴上方的部分上是否存在这样的点P.使得?若存在.求出点P的坐标,若不存在.请说明理由. (1)解法一:∵一次函数的图象与x轴交于点A ∴点A的坐标为(4.0) ∵抛物线经过O.A两点 解法二:∵一次函数的图象与x轴交于点A ∴点A的坐标为(4.0) ∵抛物线经过O.A两点 ∴抛物线的对称轴为直线 (2)解:由抛物线的对称性可知.DO=DA ∴点O在⊙D上.且∠DOA=∠DAO 又由(1)知抛物线的解析式为 ∴点D的坐标为() ①当时. 如图1.设⊙D被x轴分得的劣弧为.它沿x轴翻折后所得劣弧为.显然所在的圆与⊙D关于x轴对称.设它的圆心为D' ∴点D'与点D也关于x轴对称 ∵点O在⊙D'上.且⊙D与⊙D'相切 ∴点O为切点 ∴D'O⊥OD ∴∠DOA=∠D'OA=45° ∴△ADO为等腰直角三角形 ∴点D的纵坐标为 ∴抛物线的解析式为 ②当时. 同理可得: 抛物线的解析式为 综上.⊙D半径的长为.抛物线的解析式为或 (3)解答:抛物线在x轴上方的部分上存在点P.使得 设点P的坐标为(x.y).且y>0 ①当点P在抛物线上时 ∵点B是⊙D的优弧上的一点 过点P作PE⊥x轴于点E 由解得: ∴点P的坐标为 ②当点P在抛物线上时 同理可得. 由解得: ∴点P的坐标为 综上.存在满足条件的点P.点P的坐标为 或
网址:http://m.1010jiajiao.com/timu3_id_440778[举报]
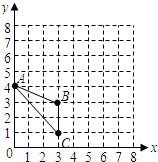 已知△ABC在平面直角坐标系中的位置如图所示.
已知△ABC在平面直角坐标系中的位置如图所示.(1)分别写出图中点A和点C的坐标;
(2)画出△ABC绕点C按顺时针方向旋转90°后再绕点B按逆时针方向旋转90°的△A′B′C′;
(3)求点A旋转到点A′所经过的路线长(结果保留π).
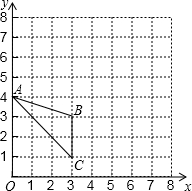 已知△ABC在平面直角坐标系中的位置如图所示.
已知△ABC在平面直角坐标系中的位置如图所示.(1)分别写出图中△ABC三个顶点的坐标;
(2)将△ABC绕点A按逆时针方向旋转90°后得到△AB′C′,请在图中画出△AB′C′;
(3)在△ABC的旋转过程中,求线段BC扫过的面积.(结果保留π).
已知:在平面直角坐标系中,Rt△ABO如图所示,点B在y轴上,且OB=4,sinA=
,若反比例函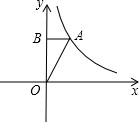 数y=
数y=
(x>0)的图象恰好过点A.
(1)求点A的坐标及反比例函数y=
(x>0)的解析式.
(2)将△ABO沿直线y=x翻折,折叠后点B的对应点为B′,点A的对应点为A′,求翻折后点B′的坐标,并判断点A′是否落在反比例函数y=
(x>0)的图象上?并说明理由.
查看习题详情和答案>>
| 4 |
| 5 |
 数y=
数y=| k |
| x |
(1)求点A的坐标及反比例函数y=
| k |
| x |
(2)将△ABO沿直线y=x翻折,折叠后点B的对应点为B′,点A的对应点为A′,求翻折后点B′的坐标,并判断点A′是否落在反比例函数y=
| k |
| x |
 已知△ABC在平面直角坐标系中的位置如图所示.
已知△ABC在平面直角坐标系中的位置如图所示. 18、已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度).
18、已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度).