摘要：直线y =+2与x轴交于B.与轴交于A.⊙0是△ABO的外接圆∠BAO的平分线交OC于点D连BD.OD.求: 在坐标轴上求点E.使△ODE与△OAB相似.
网址：http://m.1010jiajiao.com/timu3_id_439876[举报]
直线l的解析式为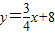
，与x轴、y轴分别交于A、B两点，P是x轴上一点，以P为圆心的圆与直线l相切于B点．
（1）求点P的坐标及⊙P的半径R；
（2）若⊙P以每秒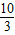
个单位沿x轴向左运动，同时⊙P的半径以每秒
个单位变小，设⊙P的运动时间为t秒，且⊙P始终与直线l有交点，试求t的取值范围；
（3）在（2）中，设⊙P被直线l截得的弦长为a，问是否存在t的值，使a最大？若存在，求出t的值；
（4）在（2）中，设⊙P与直线l的一个交点为Q，使得△APQ与△ABO相似，请直接写出此时t的值．
查看习题详情和答案>>
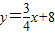，与x轴、y轴分别交于A、B两点，P是x轴上一点，以P为圆心的圆与直线l相切于B点．（1）求点P的坐标及⊙P的半径R；
（2）若⊙P以每秒
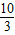个单位沿x轴向左运动，同时⊙P的半径以每秒个单位变小，设⊙P的运动时间为t秒，且⊙P始终与直线l有交点，试求t的取值范围；（3）在（2）中，设⊙P被直线l截得的弦长为a，问是否存在t的值，使a最大？若存在，求出t的值；
（4）在（2）中，设⊙P与直线l的一个交点为Q，使得△APQ与△ABO相似，请直接写出此时t的值．
查看习题详情和答案>>
直线l的解析式为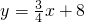
，与x轴、y轴分别交于A、B两点，P是x轴上一点，以P为圆心的圆与直线l相切于B点．
（1）求点P的坐标及⊙P的半径R；
（2）若⊙P以每秒
个单位沿x轴向左运动，同时⊙P的半径以每秒
个单位变小，设⊙P的运动时间为t秒，且⊙P始终与直线l有交点，试求t的取值范围；
（3）在（2）中，设⊙P被直线l截得的弦长为a，问是否存在t的值，使a最大？若存在，求出t的值；
（4）在（2）中，设⊙P与直线l的一个交点为Q，使得△APQ与△ABO相似，请直接写出此时
t的值．
查看习题详情和答案>>
如图，Rt△ABO的顶点A是双曲线y=
与直线y=-x-（k+1）在第二象限的交点．AB⊥x轴于B，且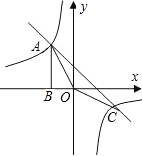
S△ABO=
．
（1）求这两个函数的解析式；
（2）求直线与双曲线的两个交点A、C的坐标和△AOC的面积． 查看习题详情和答案>>
| k |
| x |
S△ABO=| 3 |
| 2 |
（1）求这两个函数的解析式；
（2）求直线与双曲线的两个交点A、C的坐标和△AOC的面积． 查看习题详情和答案>>
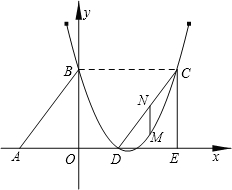如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为（-3，0）、（0，4），抛物线y=
如图，Rt△ABO的顶点A是双曲线y=