摘要：如图.以BC为直径的半圆与AB.AC相交于D.E. 设△ADE.△ABC的面积分别为S1,S2,则等于( ) A sinA B sin2A C cosA D cos2A
网址：http://m.1010jiajiao.com/timu3_id_438365[举报]
如图，△ABC中，AC=BC，以BC上一点O为圆心、OB为半径作⊙O交AB于点D．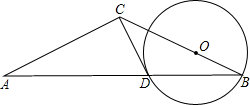
已知经过点D的⊙O切线恰好经过点C．
（1）试判断CD与AC的位置关系，并证明；
（2）若△ACB∽△CDB，且AC=3，求圆心O到直线AB的距离． 查看习题详情和答案>>
已知经过点D的⊙O切线恰好经过点C．（1）试判断CD与AC的位置关系，并证明；
（2）若△ACB∽△CDB，且AC=3，求圆心O到直线AB的距离． 查看习题详情和答案>>
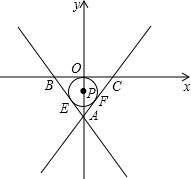
如图，等边△ABC的边长为2
，以BC边所在直线为x轴，BC边上的高线AO所在的直线为y轴建立平面直角坐标系．
（1）求过A、B、C三点的抛物线的解析式．
（2）如图，设⊙P是△ABC的内切圆，分别切AB、AC于E、F点，求阴影部分的面积．
（3）点D为y轴上一动点，当以D点为圆心，3为半径的⊙D与直线AB、AC都相切时，试判断⊙D与（2）中⊙P的位置关系，并简要说明理由．
（4）若（2）中⊙P的大小不变，圆心P设y轴运动，设P点坐标为（0，a），则⊙P与直线AB、AC有几种位置关系？并写出相应位置关系时a的取值范围．
查看习题详情和答案>>
| 3 |
（1）求过A、B、C三点的抛物线的解析式．
（2）如图，设⊙P是△ABC的内切圆，分别切AB、AC于E、F点，求阴影部分的面积．
（3）点D为y轴上一动点，当以D点为圆心，3为半径的⊙D与直线AB、AC都相切时，试判断⊙D与（2）中⊙P的位置关系，并简要说明理由．
（4）若（2）中⊙P的大小不变，圆心P设y轴运动，设P点坐标为（0，a），则⊙P与直线AB、AC有几种位置关系？并写出相应位置关系时a的取值范围．
查看习题详情和答案>>
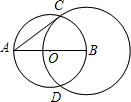如图，AB是⊙O的直径，AB=10，以B为圆心画圆．（1）若⊙B和⊙O相交，设交点为 C、D；
①试判断直线AC与⊙B的关系，并说明理由；
②若⊙B的半径是6，连接CO、OD、DB、BC，求四边形CODB的面积；
（2）若⊙B与⊙O相切，则⊙B的半径=
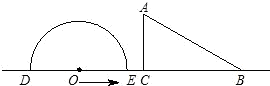
如图，Rt△ABC中，∠C=90°，O为AB上一点，以O为圆心，OA为半径作圆O与BC相切于点D，分别交AC、AB于E、F，若CD=2CE=4，则⊙O的直径为