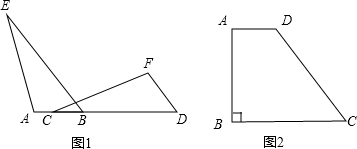
摘要:25.如图19.在梯形ABCD中.AD∥BC.BD=CD.AB<CD 且∠ABC为锐角.若AD=4.BC=12.E为BC上一点. 问:当CE分别为何值时.四边形ABED是等腰梯形?直角梯形? 请分别说明理由.
网址:http://m.1010jiajiao.com/timu3_id_437466[举报]
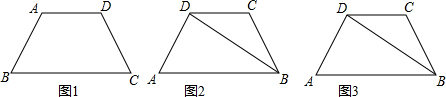
22、(1)沿等腰直角△ABC的中位线DE剪开,把分割成的两部分拼成如图1的四边形BCDD′,是一个特殊的平行四边形,你认为四边形BCDD′一定是
(2)如图2,沿等腰直角△ABC任一条中位线剪开,把分割成的两部分拼一个与图6不同的四边形,画出图形,并说明四边形的名称;
(3)如图3,在梯形ABCD中,沿一条直线剪开,把分割成的两部分拼成一个三角形,画出你拼得的图形.
(本题画图的工具不限,不必写画法和证明,但必须保留画图痕迹)

查看习题详情和答案>>
矩形
;(2)如图2,沿等腰直角△ABC任一条中位线剪开,把分割成的两部分拼一个与图6不同的四边形,画出图形,并说明四边形的名称;
(3)如图3,在梯形ABCD中,沿一条直线剪开,把分割成的两部分拼成一个三角形,画出你拼得的图形.
(本题画图的工具不限,不必写画法和证明,但必须保留画图痕迹)

(2013•阜宁县一模)在数学学习和研究中经常需要总结运用数学思想方法.如类比、转化、从特殊到一般等思想方法,如下是一个案例,请补充完整.
题目:如图1,在平行四边形ABCD中,点E是BC的中点,点F在线段AE上,BF的延长线交射线CD于点G,若
=3,求
的值.

(1)尝试探究
在图1中,过点E作EH∥AB交BG于点H,则易求
的值是
的值是
的值是
.
(2)类比延伸
如图2,在原题的条件下,若
=m(m>0),则
的值是
.(用含m的代数式表示),写出解答过程.
(3)拓展迁移
如图3,在梯形ABCD中,DC∥AB,点E是BC延长线上的一点,AE和BD相交于F,若
=a,
=b(a>0,b>0),则
的值是
查看习题详情和答案>>
题目:如图1,在平行四边形ABCD中,点E是BC的中点,点F在线段AE上,BF的延长线交射线CD于点G,若
| AF |
| EF |
| CD |
| CG |

(1)尝试探究
在图1中,过点E作EH∥AB交BG于点H,则易求
| AB |
| EH |
3
3
,| CG |
| EH |
2
2
,从而确定| CD |
| CG |
| 3 |
| 2 |
| 3 |
| 2 |
(2)类比延伸
如图2,在原题的条件下,若
| AF |
| EF |
| CD |
| CG |
| m |
| 2 |
| m |
| 2 |
(3)拓展迁移
如图3,在梯形ABCD中,DC∥AB,点E是BC延长线上的一点,AE和BD相交于F,若
| AB |
| CD |
| BC |
| BE |
| AF |
| EF |
ab
ab
.(用含a、b的代数式表示)写出解答过程.(2012•黑河)如图1,在正方形ABCD中,点M、N分别在AD、CD上,若∠MBN=45°,易证MN=AM+CN
(1)如图2,在梯形ABCD中,BC∥AD,AB=BC=CD,点M、N分别在AD、CD上,若∠MBN=
∠ABC,试探究线段MN、AM、CN有怎样的数量关系?请写出猜想,并给予证明.
(2)如图3,在四边形ABCD中,AB=BC,∠ABC+∠ADC=180°,点M、N分别在DA、CD的延长线上,若∠MBN=
∠ABC,试探究线段MN、AM、CN又有怎样的数量关系?请直接写出猜想,不需证明.

查看习题详情和答案>>
(1)如图2,在梯形ABCD中,BC∥AD,AB=BC=CD,点M、N分别在AD、CD上,若∠MBN=
| 1 |
| 2 |
(2)如图3,在四边形ABCD中,AB=BC,∠ABC+∠ADC=180°,点M、N分别在DA、CD的延长线上,若∠MBN=
| 1 |
| 2 |