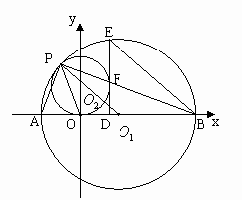
摘要:41.已知:如图.直线交轴于.交轴于.⊙与轴相切于O点.交直线于P点.以为圆心P为半径的圆交轴于A.B两点.PB交⊙于点F.⊙的弦BE=BO.EF的延长线交AB于D.连结PA.PO. (1)求证:, (2)求证:EF是⊙的切线, (3)的延长线交⊙于C点.若G为BC上一动点.以为直径作⊙交于点M.交于N.下列结论①为定值,②线段MN的长度不变.只有一个是正确的.请你判断出正确的结论.并证明正确的结论.以及求出它的值.
网址:http://m.1010jiajiao.com/timu3_id_437342[举报]
已知:如图,直线![]() 交
交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() ,⊙
,⊙![]() 与
与![]() 轴相切于O点,交直线
轴相切于O点,交直线![]()
![]() 于P点,以
于P点,以![]() 为圆心
为圆心![]() P为半径的圆交
P为半径的圆交![]() 轴于A、B两点,PB交⊙
轴于A、B两点,PB交⊙![]() 于点F,⊙
于点F,⊙![]() 的弦BE=BO,EF的延长线交AB于D,连结PA、PO。
的弦BE=BO,EF的延长线交AB于D,连结PA、PO。
(1
)求证:(2
)求证:EF是⊙(3
) 
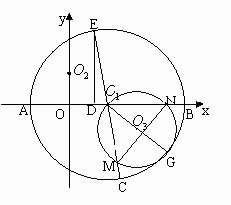
已知:如图,抛物线y=
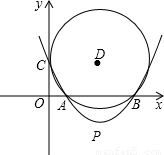
x2-3x+c交x轴正半轴于A、B两点,交y轴于C点,过A、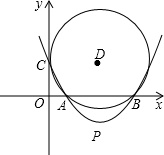 B、C三点作⊙D.若⊙D与y轴相切.
B、C三点作⊙D.若⊙D与y轴相切.
(1)求c的值;
(2)连接AC、BC,设∠ACB=α,求tanα;
(3)设抛物线顶点为P,判断直线PA与⊙D的位置关系,并证明. 查看习题详情和答案>>
| 1 | 2 |
 B、C三点作⊙D.若⊙D与y轴相切.
B、C三点作⊙D.若⊙D与y轴相切.(1)求c的值;
(2)连接AC、BC,设∠ACB=α,求tanα;
(3)设抛物线顶点为P,判断直线PA与⊙D的位置关系,并证明. 查看习题详情和答案>>
已知:如图,抛物线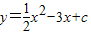 交x轴正半轴于A、B两点,交y轴于C点,过A、B、C三点作⊙D.若⊙D与y轴相切.
交x轴正半轴于A、B两点,交y轴于C点,过A、B、C三点作⊙D.若⊙D与y轴相切.
(1)求c的值;
(2)连接AC、BC,设∠ACB=α,求tanα;
(3)设抛物线顶点为P,判断直线PA与⊙D的位置关系,并证明.
 查看习题详情和答案>>
查看习题详情和答案>>
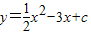 交x轴正半轴于A、B两点,交y轴于C点,过A、B、C三点作⊙D.若⊙D与y轴相切.
交x轴正半轴于A、B两点,交y轴于C点,过A、B、C三点作⊙D.若⊙D与y轴相切.(1)求c的值;
(2)连接AC、BC,设∠ACB=α,求tanα;
(3)设抛物线顶点为P,判断直线PA与⊙D的位置关系,并证明.
 查看习题详情和答案>>
查看习题详情和答案>>
 交x轴正半轴于A、B两点,交y轴于C点,过A、B、C三点作⊙D.若⊙D与y轴相切.
交x轴正半轴于A、B两点,交y轴于C点,过A、B、C三点作⊙D.若⊙D与y轴相切.
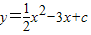 交x轴正半轴于A、B两点,交y轴于C点,过A、B、C三点作⊙D.若⊙D与y轴相切.
交x轴正半轴于A、B两点,交y轴于C点,过A、B、C三点作⊙D.若⊙D与y轴相切.