摘要：30． 如图.平面直角坐标系中.四边形OABC为矩形.点A.B的坐标分别为.动点M.N分别从O.B同时出发.以每秒1个单位的速度运动.其中.点M沿OA向终点A运动.点N沿BC向终点C运动.过点N作NP⊥BC.交AC于P.连结MP. 已知动点运动了秒. (1)P点的坐标为( . ), (2)试求 △MPA面积的最大值.并求此时x的值. (3)请你探索:当x为何值时.△MPA是一个等腰三角形? 你发现了几种情况?写出你的研究成果.
网址：http://m.1010jiajiao.com/timu3_id_437053[举报]
如图，在平面直角坐标系中，矩形ABCO的面积为15，边OA比OC大2．E为BC的中点，以OE为直径的⊙O′交
轴于D点，过点D作DF⊥AE于点F。
（1）求OA、OC的长；
（2）求证：DF为⊙O′的切线；
（3）小明在解答本题时，发现△AOE是等腰三角形。由此，他断定：“直线BC上一定存在除点E以外的点P，使△AOP也是等腰三角形，且点P一定在⊙O′外”。你同意他的看法吗？请充分说明理由。
查看习题详情和答案>>
如图，在平面直角坐标系中，矩形ABCO的面积为15，边OA比OC大2．E为BC的中点，以OE为直径的⊙O′交
轴于D点，过点D作DF⊥AE于点F。
（1）求OA、OC的长；
（2）求证：DF为⊙O′的切线；
（3）小明在解答本题时，发现△AOE是等腰三角形。由此，他断定：“直线BC上一定存在除点E以外的点P，使△AOP也是等腰三角形，且点P一定在⊙O′外”。你同意他的看法吗？请充分说明理由。
查看习题详情和答案>>
（本小题满分7分）如图，平面直角坐标系中，点A、B、C在x轴上，点D、E在y轴上，OA=OD=2，OC=OE=4，2OB=OD，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合)，
PQ∥y轴与抛物线交于点Q.
【小题1】 (1)求经过B、E、C三点的抛物线的解析式；
【小题2】 (2)是否存在点P，使得以P、Q、M为顶点的三角形与△AOD相似？若存在，求出满足条件的点P的坐标；若不存在，请说明理由； 查看习题详情和答案>>
PQ∥y轴与抛物线交于点Q.
 |
【小题1】 (1)求经过B、E、C三点的抛物线的解析式；
【小题2】 (2)是否存在点P，使得以P、Q、M为顶点的三角形与△AOD相似？若存在，求出满足条件的点P的坐标；若不存在，请说明理由； 查看习题详情和答案>>
如图，在平面直角坐标系中，矩形ABCO的面积为15，边OA比OC大2．E为BC的中点，以OE为直径的⊙O′交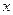
轴于D点，过点D作DF⊥AE于点F。
（1）求OA、OC的长；
（2）求证：DF为⊙O′的切线；
（3）小明在解答本题时，发现△AOE是等腰三角形。由此，他断定：“直线BC上一定存在除点E以外的点P，使△AOP也是等腰三角形，且点P一定在⊙O′外”。你同意他的看法吗？请充分说明理由。 查看习题详情和答案>>
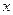轴于D点，过点D作DF⊥AE于点F。（1）求OA、OC的长；
（2）求证：DF为⊙O′的切线；
（3）小明在解答本题时，发现△AOE是等腰三角形。由此，他断定：“直线BC上一定存在除点E以外的点P，使△AOP也是等腰三角形，且点P一定在⊙O′外”。你同意他的看法吗？请充分说明理由。 查看习题详情和答案>>
（本小题满分7分）如图，平面直角坐标系中，点A、B、C在x轴上，点D、E在y轴上，OA=OD=2，OC=OE=4，2OB=OD，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合)，
PQ∥y轴与抛物线交于点Q.
 |
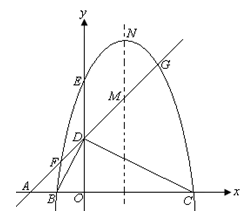【小题1】 (1)求经过B、E、C三点的抛物线的解析式；
【小题2】 (2)是否存在点P，使得以P、Q、M为顶点的三角形与△AOD相似？若存在，求出满足条件的点P的坐标；若不存在，请说明理由； 查看习题详情和答案>>