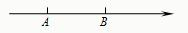摘要:如图.A和B是外离两圆.⊙A的半径为2.⊙B的半径为1.AB=4.P为连结两圆圆心的线段AB上一点.PC切⊙A于点C.PD切⊙B于点D. (1)若PC=PD.求PB的长 (2)试问线段AB上是否存在一点P.使PC2+PD2=4?如果存在.问这样的P点有几个?并求出PB的值,如果不存在.说明理由. (3)当点P在线段AB上运动到某处.使PC⊥PD时.就有△APC∽△PBD.请问:除上述情况外.当点P在线段AB上运动到何处(说明PB的长为多少,或PC.PD具有何种关系)时.这两个三角形仍相似,并判断此时直线CP与⊙B的位置关系.证明你的结论.
网址:http://m.1010jiajiao.com/timu3_id_436670[举报]
已知两圆的半径分别为R和r(R>r),圆心距为d.如图,若数轴上的点A表示R-r,点B表示R+r,当两圆外离时,表示圆心距d的点D所在的位置是( )

A.在点B右侧
B.与点B重合
C.在点A和点B之间
D.在点A左侧
查看习题详情和答案>>

A.在点B右侧
B.与点B重合
C.在点A和点B之间
D.在点A左侧
查看习题详情和答案>>
已知两圆的半径分别为R和r(R>r),圆心距为d.如图,若数轴上的点A表示R-r,点B表示R+r,当两圆外离时,表示圆心距d的点D所在的位置是( )

A.在点B右侧
B.与点B重合
C.在点A和点B之间
D.在点A左侧
查看习题详情和答案>>

A.在点B右侧
B.与点B重合
C.在点A和点B之间
D.在点A左侧
查看习题详情和答案>>