摘要:如图.将▱ABCD的边DC延长到点E.使CE=DC.连接AE.交BC于点F. (1)求证:△ABF≌△ECF, (2)若∠AFC=2∠D.连接AC.BE.求证:四边形ABEC是矩形. 考点:平行四边形的判定与性质,全等三角形的判定与性质,矩形的判定. 专题:证明题. 分析:(1)先由已知平行四边形ABCD得出AB∥DC.AB=DC.⇒∠ABF=∠ECF.从而证得△ABF≌△ECF, 得的结论先证得四边形ABEC是平行四边形.通过角的关系得出FA=FE=FB=FC.AE=BC.得证. 解答:证明:(1)∵四边形ABCD是平行四边形. ∴AB∥DC.AB=DC. ∴∠ABF=∠ECF. ∵EC=DC.∴AB=EC. 在△ABF和△ECF中. ∵∠ABF=∠ECF.∠AFB=∠EFC.AB=EC. ∴△ABF≌△ECF. (2)∵AB=EC.AB∥EC. ∴四边形ABEC是平行四边形. ∴FA=FE.FB=FC. ∵四边形ABCD是平行四边形. ∴∠ABC=∠D. 又∵∠AFC=2∠D. ∴∠AFC=2∠ABC. ∵∠AFC=∠ABF+∠BAF. ∴∠ABF=∠BAF. ∴FA=FB. ∴FA=FE=FB=FC. ∴AE=BC. ∴四边形ABEC是矩形. 点评:此题考查的知识点是平行四边形的判定与性质.全等三角形的判定和性质及举行的判定.关键是先由平行四边形的性质证三角形全等.然后推出平行四边形通过角的关系证矩形.
网址:http://m.1010jiajiao.com/timu3_id_436020[举报]
 如图,将两个完全一样含有30°角的直角三角板如图摆放(点D、B、C在一条直线上),∠A与∠D为30°角,∠ABC与∠DCE为直角.
如图,将两个完全一样含有30°角的直角三角板如图摆放(点D、B、C在一条直线上),∠A与∠D为30°角,∠ABC与∠DCE为直角.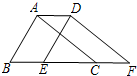 如图,将周长为8cm的△ABC沿BC方向平移1cm得到△DEF,则四边形ABFD周长为( )
如图,将周长为8cm的△ABC沿BC方向平移1cm得到△DEF,则四边形ABFD周长为( ) 如图,将边长为2的正方形ABCD放在直线l上且沿着l向右做无滑动地翻滚,当正方形ABCD翻滚一周时,则它的中心点O所经过的路线长是
如图,将边长为2的正方形ABCD放在直线l上且沿着l向右做无滑动地翻滚,当正方形ABCD翻滚一周时,则它的中心点O所经过的路线长是 如图,将一把宽2cm的直尺如图放置,直尺经过圆心O且与⊙O分别交于点A、B、C、D.若AB=8cm,则CD=
如图,将一把宽2cm的直尺如图放置,直尺经过圆心O且与⊙O分别交于点A、B、C、D.若AB=8cm,则CD= 到点1000距离相等的点表示的数是
到点1000距离相等的点表示的数是