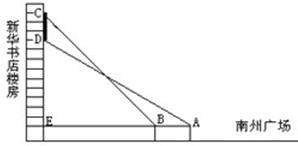
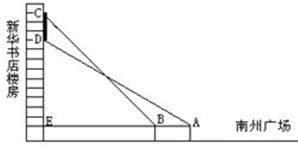
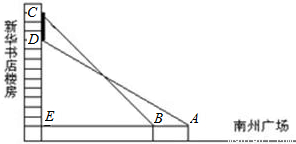
摘要:如图.小刚同学在綦江南州广场上观测新华书店楼房墙上的电子屏幕CD.点A是小刚的眼睛.测得屏幕下端D处的仰角为30°.然后他正对屏幕方向前进了6米到达B处.又测得该屏幕上端C处的仰角为45°.延长AB与楼房垂直相交于点E.测得BE=21米.请你帮小刚求出该屏幕上端与下端之间的距离CD. 考点:解直角三角形的应用-仰角俯角问题. 专题:应用题. 分析:易得CE=BE.利用30°的正切值即可求得CE长.进而可求得DE长.CE减去DE长即为广告屏幕上端与下端之间的距离. 解答:解:∵∠CBE=45°.CE⊥AE. ∴CE=BE. ∴CE=21. ∴AE=AB+BE=21+6=27. 在Rt△ADE中.∠DAE=30°. ∴DE=AE×tan30°=27×=9. ∴CD=CE﹣DE=21﹣9. 答:广告屏幕上端与下端之间的距离约为21﹣9m. 点评:本题考查了仰角的定义.要求学生能借助仰角构造直角三角形并解直角三角形,难点是充分找到并运用题中相等的线段.
网址:http://m.1010jiajiao.com/timu3_id_435666[举报]
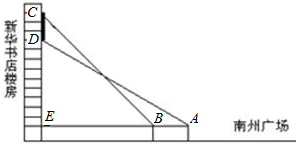
如图,小刚同学在綦江南州广场上观测新华书店楼房墙上的电子屏幕CD,点A是小刚的眼睛,测得屏幕下端D处的仰角为30°,然后他正对屏幕方向前进了6米到达B处,又测得该屏幕上端C处的仰角为45°,延长AB与楼房垂直相交于点E,测得BE=21米,请你帮小刚求出该屏幕上端与下端之间的距离CD.(结果保留根号)
 查看习题详情和答案>>
查看习题详情和答案>>
 查看习题详情和答案>>
查看习题详情和答案>>
(2011•綦江县)如图,小刚同学在綦江南州广场上观测新华书店楼房墙上的电子屏幕CD,点A是小刚的眼睛,测得屏幕下端D处的仰角为30°,然后他正对屏幕方向前进了6米到达B处,又测得该屏幕上端C处的仰角为45°,延长AB与楼房垂直相交于点E,测得BE=21米,请你帮小刚求出该屏幕上端与下端之间的距离CD.(结果保留根号)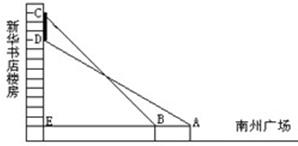 查看习题详情和答案>>
查看习题详情和答案>>
 查看习题详情和答案>>
查看习题详情和答案>>
(2011•綦江县)如图,小刚同学在綦江南州广场上观测新华书店楼房墙上的电子屏幕CD,点A是小刚的眼睛,测得屏幕下端D处的仰角为30°,然后他正对屏幕方向前进了6米到达B处,又测得该屏幕上端C处的仰角为45°,延长AB与楼房垂直相交于点E,测得BE=21米,请你帮小刚求出该屏幕上端与下端之间的距离CD.(结果保留根号)