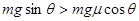摘要： 解:(1)小物块受力平衡 qE＝mgtan37° 故E＝ -2分 (2)场强变化后物块所受合力为 F＝mgsin37°-qEcos37° F=ma 故a=0.3g--------------2分 (3)动能Ek=mgLsin37°-qEL cos37°= 0.3mgL-----3分
网址：http://m.1010jiajiao.com/timu3_id_1623645[举报]
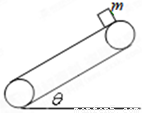
如图所示，传送带与水平面的夹角θ，当传送带静止时，在传送带顶端静止释放小物块m，小物块沿传送带滑到底端需要的时间为t0，已知小物块与传送带间的动摩擦因数为μ．则下列说法正确的是（ ）
查看习题详情和答案>>
如图所示，传送带与水平面的夹角θ，当传送带静止时，在传送带顶端静止释放小物块m，小物块沿传送带滑到底端需要的时间为t0，已知小物块与传送带间的动摩擦因数为μ。则下列说法正确的是（ ）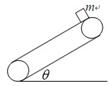
A．传送带静止时，小物块受力应满足 |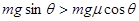
| B．若传送带顺时针转动，小物块将不可能沿传送带滑下到达底端 |
| C．若传送带顺时针转动，小物块将仍能沿传送带滑下，且滑到底端的时间等于t0 |
| D．若传送带逆时针转动，小物块滑到底端的时间小于t0 |
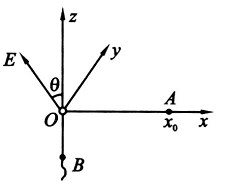
（25分）如图所示，
轴竖直向上，
平面是一绝缘的、固定的、刚性平面。在
处放一带电量为
的小物块，该物块与一细线相连，细线的另一端
穿过位于坐标原点
的光滑小孔，可通过它牵引小物块。现对该系统加一匀强电场，场强方向垂直与
轴，与轴夹角为
（如所示）。设小物块和绝缘平面间的摩擦系数为
,且静摩擦系数和滑动摩擦系数相同。不计重力作用。现通过细线来牵引小物块，使之移动。在牵引过程中，我们约定：细线的端只准沿轴向下缓慢移动，不得沿轴向上移动；小物块的移动非常缓慢，在任何时刻，都可近似认为小物块处在力平衡状态。若已知小物块的移动轨迹是一条二次曲线，试求出此轨迹方程。
