摘要：14．如图.有一电阻不计.质量为m的金属棒ab.可在两条轨道上滑动.轨道宽为L,轨道平面与水平面间的夹角为θ.置于垂直轨道平面向上的匀强磁场中.磁感应强度的大小为B.金属棒与轨道间的最大静磨擦力为重力的k倍.回路中电源电动势为E,内阻不计.轨道电阻也不计.问:滑动变阻器调节在什么阻值范围内.金属棒能静止在轨道上?
网址：http://m.1010jiajiao.com/timu3_id_1606783[举报]
如图6-1-10 所示，有一电阻不计、质量为m的金属棒ab可在两条轨道上滑动，轨道宽为L，轨道平面与水平面间夹角为θ，置于垂直轨道平面向上的匀强磁场中，磁感应强度大小为B.金属棒与轨道间的最大静摩擦力为重力的k倍，回路中电源电动势为E，内阻不计，轨道电阻也不计.问：滑动变阻器调节在什么阻值范围内，金属棒恰能静止在轨道上？
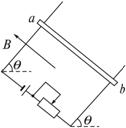
图
如图3-4-34所示，有一电阻不计、质量为m的金属棒ab可在两条轨道上滑动，轨道宽为L，轨道平面与水平面间夹角为θ，置于垂直轨道平面向上的匀强磁场中，磁感应强度大小为B.金属棒与轨道间的最大静摩擦力为重力的k倍，回路中电源电动势为E，内阻不计，轨道电阻也不计.问：滑动变阻器调节在什么阻值范围内，金属棒恰能静止在轨道上？
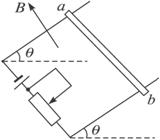
图3-4-34
查看习题详情和答案>>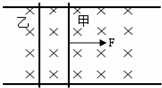
如图，两根足够长的平行金属导轨，固定在同一水平面上，导轨的电阻很小，可忽略不计．导轨间的距离L=0.2m．磁感应强度B=0.50T的匀强磁场与导轨所在平面垂直．两根质量均为m=0.10kg的平行金属杆甲、乙可在动摩擦因素μ=0.1的导轨上滑动，滑动过程中与导轨保持垂直，每根金属杆的电阻为R=0.50Ω．开始时两根金属杆都处于静止状态．现有一与导轨平行、大小为0.20N的恒力F作用于金属杆甲上，使金属杆甲在导轨上滑动．试分析并求出经过相当长时间后两杆与导轨组成的闭合回路中的电功率（设最大静摩擦力等于滑动摩擦力）．
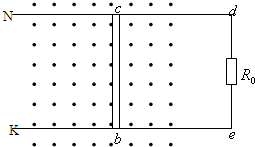如图，在一水平面内有两根平行的金属导轨Nd、Ke，其电阻不计，导轨上有一根金属棒bc，长L=0.5m，质量m=0.1kg，与导轨接触良好，可在导轨上无摩擦地滑动，bc的电阻R=0.2Ω．竖直向上的匀强磁场磁感应强度B=0.1T，导轨的右端接有电阻R0=0.3Ω，导轨左端足够长．（1）给棒bc外加一个水平向左的拉力，使其从静止开始向左作加速度为a=4m/s2的匀变速直线运动，运动到5s末时，这个拉力为多大？
（2）若把拉力刚作用于静止的bc棒的时刻取为计时的0时刻，拉力大小变化规律为F=（2.5×10-2t+0.5）N，式中t的单位是秒，拉力的方向水平向左，经过一段时间，力F对bc棒做功54J，试论证在这段时间内电阻R0上的发热量小于32.4J．
（3）在第（2）问的条件下，bc棒的加速度只能是以下两种情况中一种．请你判断哪种情况是正确的，并按相应要求作答：（不要求写出作判断的推理过程）
（Ⅰ）bc的加速度恒定（请求出这个加速度的大小）
（Ⅱ）bc的加速度变化（请定性地指出这个加速度的增减情况）
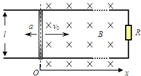如图，两条互相平行且足够长的光滑金属导轨位于水平面内，导轨间距l=0.2m，在导轨的一端接有阻值R=3Ω的电阻，在x≥0处有一垂直水平面向下的匀强磁场，磁感强度B=0.5T．一质
量m=0.1kg，电阻r=2Ω的金属棒垂直搁在导轨上，并以v0=20m/s的初速度进入磁场，在水平拉
力F的作用下作持续的匀变速直线运动，加速度大小a=2m/s2、方向与初速度方向相反．棒与导轨
接触良好，其余电阻均不计．求：
（1）第一次电流为零时金属棒所处的位置；
（2）电流为最大值的一半时拉力F的大小及其功率；
（3）金属棒开始进入磁场到速度减小为零的过程中，电阻R上产生的热量为1.6J，求该过程中拉力F所做的功．