摘要:如图9-1所示.质量为M=3kg的木板静止在光滑水平面上.板的右端放一质量为m=1kg的小铁块.现给铁块一个水平向左速度V0=4m/s.铁块在木板上滑行.与固定在木板左端的水平轻弹簧相碰后又返回.且恰好停在木板右端.求铁块与弹簧相碰过程中.弹性势能的最大值EP. 分析与解:在铁块运动的整个过程中.系统的动量守恒.因此弹簧压缩最大时和铁块停在木板右端时系统的共同速度可用动量守恒定律求出.在铁块相对于木板往返运动过程中.系统总机械能损失等于摩擦力和相对运动距离的乘积.可利用能量关系分别对两过程列方程解出结果. 设弹簧压缩量最大时和铁块停在木板右端时系统速度分别为V和V'.由动量守恒得:mV0=V' 所以.V=V’=mV0/=1m/s 铁块刚在木板上运动时系统总动能为:EK=mV02=0.5X1X16=8J 弹簧压缩量最大时和铁块最后停在木板右端时.系统总动能都为: EK'=(M+m)V2=0.5X(3+1)X1=2J 铁块在相对于木板往返运过程中.克服摩擦力f所做的功为: Wf=f2L=EK-EK'=8-2=6J 铁块由开始运动到弹簧压缩量最大的过程中.系统机械能损失为:fs=3J 由能量关系得出弹性势能最大值为:EP=EK-EK'-fs=8-2-3=3J 说明:由于木板在水平光滑平面上运动.整个系统动量守恒.题中所求的是弹簧的最大弹性势能.解题时必须要用到能量关系.在解本题时要注意两个方面:1.是要知道只有当铁块和木板相对静止时.弹簧的弹性势能才最大,弹性势能量大时.铁块和木板的速度都不为零,铁块停在木板右端时.系统速度也不为零. 2.是系统机械能损失并不等于铁块克服摩擦力所做的功.而等于铁块克服摩擦力所做的功和摩擦力对木板所做功的差值.故在计算中用摩擦力乘上铁块在木板上相对滑动的距离.
网址:http://m.1010jiajiao.com/timu3_id_1548924[举报]
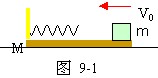
如图9-1所示,质量为M=3kg的木板静止在光滑水平面上,板的右端放一质量为m=1kg的小铁块,现给铁块一个水平向左速度V0=4m/s,铁块在木板上滑行,与固定在木板左端的水平轻弹簧相碰后又返回,且恰好停在木板右端,求铁块与弹簧相碰过程中,弹性势能的最大值EP。
如图1所示,某组同学借用“探究a与F、m之间的定量关系”的相关实验思想、原理及操作,进行“研究合外力做功和动能变化的关系”的实验:
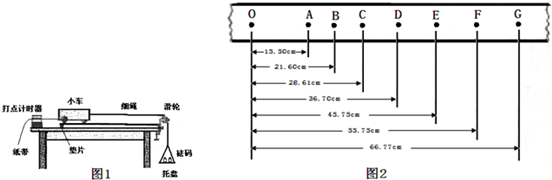
①为达到平衡阻力的目的,取下细绳及托盘,通过调整垫片的位置,改变长木板倾斜程度,根据打出的纸带判断小车是否做______运动.
②连接细绳及托盘,放人砝码,通过实验得到图2所示的纸带.纸带上0为小车运动起始时刻所打的点,选取时间间隔为0.1s的相邻计数点A、B、C、D、E、F、G.实验时小车所受拉力为0.2N,小车的质量为0.2kg.
请计算小车所受合外力做的功W和小车动能的变化△Ek,补填表中空格(结果保留至小数点后第四位).
分析上述数据可知:在实验误差允许的范围内W=△Ek,与理论推导结果一致.
③实验前已测得托盘质量为7.7×10-3kg,实验时该组同学放入托盘中的砝码质量应为______kg(g取9.8m/s2,结果保留至小数点后第三位).
查看习题详情和答案>>

①为达到平衡阻力的目的,取下细绳及托盘,通过调整垫片的位置,改变长木板倾斜程度,根据打出的纸带判断小车是否做______运动.
②连接细绳及托盘,放人砝码,通过实验得到图2所示的纸带.纸带上0为小车运动起始时刻所打的点,选取时间间隔为0.1s的相邻计数点A、B、C、D、E、F、G.实验时小车所受拉力为0.2N,小车的质量为0.2kg.
请计算小车所受合外力做的功W和小车动能的变化△Ek,补填表中空格(结果保留至小数点后第四位).
| O-B | O-C | O-D | O-E | O-F | |
| W/J | 0.0432 | 0.0572 | 0.0734 | 0.0915 | ______ |
| △Ek/J | 0.0430 | 0.0570 | 0.0734 | 0.0907 | ______ |
③实验前已测得托盘质量为7.7×10-3kg,实验时该组同学放入托盘中的砝码质量应为______kg(g取9.8m/s2,结果保留至小数点后第三位).
如图1所示,某组同学借用“探究a与F、m之间的定量关系”的相关实验思想、原理及操作,进行“研究合外力做功和动能变化的关系”的实验:
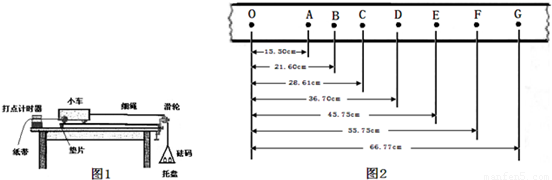
①为达到平衡阻力的目的,取下细绳及托盘,通过调整垫片的位置,改变长木板倾斜程度,根据打出的纸带判断小车是否做______运动.
②连接细绳及托盘,放人砝码,通过实验得到图2所示的纸带.纸带上0为小车运动起始时刻所打的点,选取时间间隔为0.1s的相邻计数点A、B、C、D、E、F、G.实验时小车所受拉力为0.2N,小车的质量为0.2kg.
请计算小车所受合外力做的功W和小车动能的变化△Ek,补填表中空格(结果保留至小数点后第四位).
分析上述数据可知:在实验误差允许的范围内W=△Ek,与理论推导结果一致.
③实验前已测得托盘质量为7.7×10-3kg,实验时该组同学放入托盘中的砝码质量应为______kg(g取9.8m/s2,结果保留至小数点后第三位).
查看习题详情和答案>>

①为达到平衡阻力的目的,取下细绳及托盘,通过调整垫片的位置,改变长木板倾斜程度,根据打出的纸带判断小车是否做______运动.
②连接细绳及托盘,放人砝码,通过实验得到图2所示的纸带.纸带上0为小车运动起始时刻所打的点,选取时间间隔为0.1s的相邻计数点A、B、C、D、E、F、G.实验时小车所受拉力为0.2N,小车的质量为0.2kg.
请计算小车所受合外力做的功W和小车动能的变化△Ek,补填表中空格(结果保留至小数点后第四位).
| O-B | O-C | O-D | O-E | O-F | |
| W/J | 0.0432 | 0.0572 | 0.0734 | 0.0915 | ______ |
| △Ek/J | 0.0430 | 0.0570 | 0.0734 | 0.0907 | ______ |
③实验前已测得托盘质量为7.7×10-3kg,实验时该组同学放入托盘中的砝码质量应为______kg(g取9.8m/s2,结果保留至小数点后第三位).
查看习题详情和答案>>
如图1所示,某组同学借用“探究a与F、m之间的定量关系”的相关实验思想、原理及操作,进行“研究合外力做功和动能变化的关系”的实验:
①为达到平衡阻力的目的,取下细绳及托盘,通过调整垫片的位置,改变长木板倾斜程度,根据打出的纸带判断小车是否做__________运动。
②连接细绳及托盘,放人砝码,通过实验得到图2所示的纸带。纸带上0为小车运动起始时刻所打的点,选取时间间隔为0. 1s的相邻计数点A、B、C、D、E、F、G。实验时小车所受拉力为0. 2N,小车的质量为0.2kg。
请计算小车所受合外力做的功W和小车动能的变化△Ek,补填表中空格(结果保留至小数点后第四位)。
| O-B | O-C | O-D | O-E | O-F | |
| W/J | 0.0432 | 0. 0572 | 0. 0734 | 0. 0915 | |
| △Ek/J | 0.0430 | 0. 0570 | 0. 0734 | 0. 0907 |
分析上述数据可知:在实验误差允许的范围内W= △Ek,与理论推导结果一致。
③实验前已测得托盘质量为7.7×10-3kg,实验时该组同学放入托盘中的砝码质量应为___________kg(g取9.8m/s2,结果保留至小数点后第三位)。
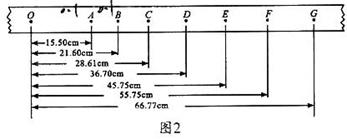
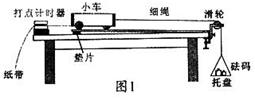
如图1所示,某组同学借用“探究a与F、m之间的定量关系”的相关实验思想、原理及操作,进行“研究合外力做功和动能变化的关系”的实验:

①为达到平衡阻力的目的,取下细绳及托盘,通过调整垫片的位置,改变长木板倾斜程度,根据打出的纸带判断小车是否做________运动.
②连接细绳及托盘,放人砝码,通过实验得到图2所示的纸带.纸带上0为小车运动起始时刻所打的点,选取时间间隔为0.1s的相邻计数点A、B、C、D、E、F、G.实验时小车所受拉力为0.2N,小车的质量为0.2kg.
请计算小车所受合外力做的功W和小车动能的变化△Ek,补填表中空格(结果保留至小数点后第四位).
| O-B | O-C | O-D | O-E | O-F | |
| W/J | 0.0432 | 0.0572 | 0.0734 | 0.0915 | ________ |
| △Ek/J | 0.0430 | 0.0570 | 0.0734 | 0.0907 | ________ |
③实验前已测得托盘质量为7.7×10-3kg,实验时该组同学放入托盘中的砝码质量应为________kg(g取9.8m/s2,结果保留至小数点后第三位). 查看习题详情和答案>>