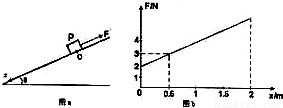
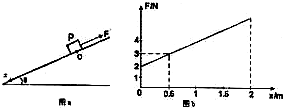如图a所示，有一个足够长的光滑斜面，倾角θ为30°，质量为0.8kg的物体置于O处．物体受到一个沿斜面向上的拉力F作用下由静止开始运动，F与x的关系如图b所示，x为物体相对于O点的位移，x轴正方向沿斜面向下，如图a所示，则：
（1）当物体位移x=0.5m时物体的加速度为多大？方向如何？
（2）当物体位移x为多大时物体的加速度最大？最大值为多少？
（3）当物体位移x为多大时物体的速度最大？最大值为多少？

如图a所示，有一个足够长的光滑斜面，倾角θ为30°，质量为0.8kg的物体置于O处．物体受到一个沿斜面向上的拉力F作用下由静止开始运动，F与x的关系如图b所示，x为物体相对于O点的位移，x轴正方向沿斜面向下，如图a所示，则：
（1）当物体位移x=0.5m时物体的加速度为多大？方向如何？
（2）当物体位移x为多大时物体的加速度最大？最大值为多少？
（3）当物体位移x为多大时物体的速度最大？最大值为多少？

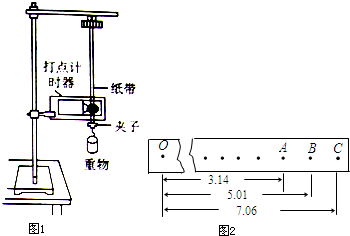
用如图1所示的实验装置验证机械能守恒定律．实验所用的电源为学生电源，输出电压为6V的交流电和直流电两种．重锤从高处由静止开始下落．重锤上拖着的纸带打出一系列的点．对纸带上的点痕进行测量，即可验证机械能守恒定律．下面列举了该实验的几个操作步骤：

A．按照图示的装置安装器件
B．将打点计时器接到电源的“直流输出”上
C．用天平测出重锤的质量
D．先释放悬挂纸带的夹子，然后接通电源打出一条纸带
E．测量纸带上某些点间的距离
F．根据测量的结果计算重锤下落过程中减少的重力势能是否等于增加的动能．
Ⅰ、其中没有必要进行的或者操作不当的步骤是．（将其选项对应的字母填在横线处）
Ⅱ、在实验中，质量m为1.0kg的重物自由下落，带动纸带打出一系列的点，如图2所示．相邻计数点间的时间间隔为0.02s，距离单位为cm．
（1）纸带的端与重物相连；
（2）打点计时器打下计数点B时，物体的速度v_B=m/s；（结果保留两位有效数字）
（3）某同学从起点O到打下计数点B的过程中，计算出物体的动能增加量△E_K=0.48J，势能减少量△E_P=0.49J（g=9.8m/s²），该同学的计算方法和过程并没有错误，却出现了△E_K＜△E_P的结果，试问这一结果是否合理？答：．
（4）另一名同学用vB2=2ghOB计算出B的动能E_K=0.49J，恰好与势能减少量△E_P相等，于是该同学得出结论“重物下落过程中机械能守恒”，试问该同学的做法是否合理？答：．