摘要:13.⑴ 2.5 m/s2 5.0 m/s2 ⑵DE区间内 ⑶设小车的质量为M.重物的质量为m.斜面的倾角为θ.小车与斜面之间的滑动摩擦力.小车加速过程中.对小车和重物整体应用牛顿第二定律得 当重物落地后.小车减速上升的过程中应用牛顿第二定律得 联立两式并将的数值代入得
网址:http://m.1010jiajiao.com/timu3_id_1541316[举报]
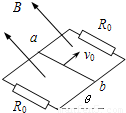
如图所示,一足够长的平面框架宽L=0.3m,与水平面成θ=37°角,上下两端各有一个电阻R=2Ω,框架其它部分的电阻不计,垂直于框架平面的方向上存在向上的匀强磁场,磁感应强度B=1T.金属杆ab长为L=0.3m,质量m=1kg,电阻r=2Ω,与框架的动摩擦因数μ=0.5,以初速度v=10m/s向上滑行.杆ab上升到最高点的过程中,上端电阻R产生的热量Q=5J,g取10m/s2,求:
(1)上升过程中,金属杆两端点ab间最大电势差的大小;
(2)ab杆沿斜面上升的最大距离;
(4)上升过程中,通过ab杆的总电荷量.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)上升过程中,金属杆两端点ab间最大电势差的大小;
(2)ab杆沿斜面上升的最大距离;
(4)上升过程中,通过ab杆的总电荷量.
 查看习题详情和答案>>
查看习题详情和答案>>
 如右图所示,一平面框架与水平面成37°角,宽L=0.4 m,上、下两端各有一个电阻R0=1 Ω,框架的其他部分电阻不计,框架足够长.垂直于框平面的方向存在向上的匀强磁场,磁感应强度B=2T.ab为金属杆,其长度为L=0.4 m,质量m=0.8 kg,电阻r=0.5Ω,棒与框架的动摩擦因数μ=0.5.由静止开始下滑,直到速度达到最大的过程中,上端电阻R0产生的热量Q0=0.375J(已知sin37°=0.6,cos37°=0.8;g取10m/s2)求:
如右图所示,一平面框架与水平面成37°角,宽L=0.4 m,上、下两端各有一个电阻R0=1 Ω,框架的其他部分电阻不计,框架足够长.垂直于框平面的方向存在向上的匀强磁场,磁感应强度B=2T.ab为金属杆,其长度为L=0.4 m,质量m=0.8 kg,电阻r=0.5Ω,棒与框架的动摩擦因数μ=0.5.由静止开始下滑,直到速度达到最大的过程中,上端电阻R0产生的热量Q0=0.375J(已知sin37°=0.6,cos37°=0.8;g取10m/s2)求:
(1)杆ab的最大速度;
(2)从开始到速度最大的过程中ab杆沿斜面下滑的距离;在该过程中通过ab的电荷量.
查看习题详情和答案>>
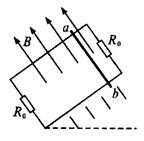 如右图所示,一平面框架与水平面成37°角,宽L=0.4 m,上、下两端各有一个电阻R0=1 Ω,框架的其他部分电阻不计,框架足够长.垂直于框平面的方向存在向上的匀强磁场,磁感应强度B=2T.ab为金属杆,其长度为L=0.4 m,质量m=0.8 kg,电阻r=0.5Ω,棒与框架的动摩擦因数μ=0.5.由静止开始下滑,直到速度达到最大的过程中,上端电阻R0产生的热量Q0=0.375J(已知sin37°=0.6,cos37°=0.8;g取10m/s2)求:
如右图所示,一平面框架与水平面成37°角,宽L=0.4 m,上、下两端各有一个电阻R0=1 Ω,框架的其他部分电阻不计,框架足够长.垂直于框平面的方向存在向上的匀强磁场,磁感应强度B=2T.ab为金属杆,其长度为L=0.4 m,质量m=0.8 kg,电阻r=0.5Ω,棒与框架的动摩擦因数μ=0.5.由静止开始下滑,直到速度达到最大的过程中,上端电阻R0产生的热量Q0=0.375J(已知sin37°=0.6,cos37°=0.8;g取10m/s2)求:
(1)杆ab的最大速度;
(2)从开始到速度最大的过程中ab杆沿斜面下滑的距离;在该过程中通过ab的电荷量.
查看习题详情和答案>>
 (2011?通州区模拟)如图所示,一足够长的平面框架宽L=0.3m,与水平面成θ=37°角,上下两端各有一个电阻R0=2Ω,框架其它部分的电阻不计,垂直于框架平面的方向上存在向上的匀强磁场,磁感应强度B=1T.金属杆ab长为L=0.3m,质量m=1kg,电阻r=2Ω,与框架的动摩擦因数μ=0.5,以初速度v0=10m/s向上滑行.杆ab上升到最高点的过程中,上端电阻R0产生的热量Q0=5J,g取10m/s2,求:
(2011?通州区模拟)如图所示,一足够长的平面框架宽L=0.3m,与水平面成θ=37°角,上下两端各有一个电阻R0=2Ω,框架其它部分的电阻不计,垂直于框架平面的方向上存在向上的匀强磁场,磁感应强度B=1T.金属杆ab长为L=0.3m,质量m=1kg,电阻r=2Ω,与框架的动摩擦因数μ=0.5,以初速度v0=10m/s向上滑行.杆ab上升到最高点的过程中,上端电阻R0产生的热量Q0=5J,g取10m/s2,求:(1)上升过程中,金属杆两端点ab间最大电势差的大小;
(2)ab杆沿斜面上升的最大距离;
(4)上升过程中,通过ab杆的总电荷量.
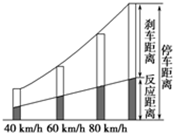 为了最大限度地减少道路交通事故,全省各地开始了“集中整治酒后驾驶违法行为”专项行动.这是因为一般驾驶员酒后的反应时间比正常时慢了0.1~0.5s,易发生交通事故.图示是《驾驶员守则》中的安全距离图示和部分安全距离表格(如图所示).
为了最大限度地减少道路交通事故,全省各地开始了“集中整治酒后驾驶违法行为”专项行动.这是因为一般驾驶员酒后的反应时间比正常时慢了0.1~0.5s,易发生交通事故.图示是《驾驶员守则》中的安全距离图示和部分安全距离表格(如图所示).| 车速v (km/h) |
反应距离 s(m) |
刹车距离 x(m) |
| 40 | 10 | 10 |
| 60 | 15 | 22.5 |
| 80 | A | 40 |
(1)请根据表格中的数据计算驾驶员的反应时间.
(2)如果驾驶员的反应时间相同,请计算出表格中A的数据.
(3)如果路面情况相同,车在刹车后所受阻力恒定,取g=10m/s2,请计算出刹车后汽车所受阻力与车重的比值.
(4)假设在同样的路面上,一名饮了少量酒后的驾驶员驾车以72km/h速度行驶,在距离一学校门前52m处发现有一队学生在斑马线上横过马路,他的反应时间比正常时慢了0.2s,会发生交通事故吗?