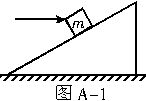
摘要:4.图1-1所示.质量为M的物体.在与竖直线成θ角.大小为F的恒力作用 下.沿竖直墙壁匀速下滑.物体与墙壁间的动摩擦因数为μ.则物体受到的 摩擦力大小是 A.Mg-Fcosθ B.μMg+Fcosθ C.Fsinθ D.μ(Mg-Fcosθ)
网址:http://m.1010jiajiao.com/timu3_id_1540949[举报]
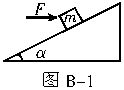
如图1-4所示,质量为m![]() 的物体A在沿斜面向上的拉力F作用下沿斜面匀速下滑,此过程斜面体B仍静止,斜面体的质量为M,则水平地面对斜面体( )
的物体A在沿斜面向上的拉力F作用下沿斜面匀速下滑,此过程斜面体B仍静止,斜面体的质量为M,则水平地面对斜面体( )
A.无摩擦力 B.有水平向左的摩擦力
C.支持力为(![]() m+M)g D.支持力小于(m+M)g
m+M)g D.支持力小于(m+M)g

![]()
图1-4
查看习题详情和答案>>
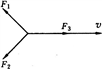
如图所示,质量为m的物体,在大小分别为F1,F2,F3的三个共点力的作用下沿F3的方向做匀速直线运动,则
(1)若只撤去力F1,物体将做____运动,这时加速度的大小为____m/s2,方向____;
(2)若只撤去力F2,物体将做____运动,这时加速度的大小为____m/s2,方向____;
(3)若只撤去力F3,物体将做____运动,这时加速度方向____.
(1)若只撤去力F1,物体将做____运动,这时加速度的大小为____m/s2,方向____;
(2)若只撤去力F2,物体将做____运动,这时加速度的大小为____m/s2,方向____;
(3)若只撤去力F3,物体将做____运动,这时加速度方向____.
如图所示,质量为M的物体,在合外力F 的作用下,在一条直线上做匀加速直线运动,物体的初速度为v0 ,加速度大小为a,经过时间t后物体的末速度为vt ,通过的位移s,解答下列问题:
![]()
(1)由匀变速直线运动的速度公式和位移公式推出![]()
(2)写出t/2时刻的即时速度表达式
(3)等式 s = vt t --![]() at2是否成立?给出较合理的解释
at2是否成立?给出较合理的解释
(4)由运动学公式和牛顿第二定律推出动能定理表达式。
查看习题详情和答案>>