摘要:(二)牛顿第二定律在系统中的应用 牛顿第二定律不仅适用于单个物体.同样也适用于系统.下面总结如下: 1. 若系统内各物体具有相同的加速度时.应先把这个系统当作一个整体.分析其受到的外力及运动情况.利用牛顿第二定律求出加速度.若求系统内各物体之间的作用力.应先把物体进行隔离.对某个物体进行单独受力分析.再利用牛顿第二定律解决: [例1] 如图1所示.A.B两滑环分别套在间距为1m的光滑细杆上.A和B的质量之比为1:3.用一自然长度为1m的轻弹簧将两环相连.在A环上作用一沿杆方向的.大小为20N的拉力F.当两环都沿杆以相同的加速度a运动时.弹簧与杆夹角为53°.求: (1)弹簧的劲度系数为多少? (2)若突然撤去拉力F.在撤去拉力F的瞬间.A的加速度为a′.a′与a之比为多少? 图1 分析: (1)先取A+B和弹簧整体为研究对象.弹簧弹力为内力.杆对A.B支持力与加速度方向垂直.在沿F方向应用牛顿第二定律 ① 再取B为研究对象 ② ①②联立求解得 由几何关系得.弹簧的伸长量 所以弹簧的劲度系数. (2)撤去力F瞬间.弹簧弹力不变.A的加速度 比较上式 点评:两者具有相同的加速度.先利用整体法求出加速度.再用隔离法问题迎刃而解.本题为瞬时加速度问题.正确进行各阶段受力分析是解题的关键.弹簧弹力与绳子弹力的区别在于前者弹力改变需时间.而后者改变不计时间. 练1:如图2所示.质量为M的斜面A置于粗糙水平地面上.动摩擦因数为.物体B与斜面间无摩擦.在水平向左的推力F作用下.A与B一起做匀加速直线运动.两者无相对滑动.已知斜面的倾角为.物体B的质量为m.则它们的加速度a及推力F的大小为( ) A. B. C. D. 图2 答案与提示:先对整体进行分析.利用牛顿第二定律隔离物体B受力求出加速度.化简后知C正确. 2. 若系统内有几个物体.这几个物体的质量分别为...-.加速度分别为...-.这个系统的合外力为.则这个系统的牛顿第二定律的表达式为 .若一个系统内各物体的加速度大小不相同.而又不需要求系统内物体间的相互作用力时.对系统整体列式子.可减少未知的内力.简化数学运算. [例2] 质量为和表面粗糙的物体叠放在粗糙的水平地面上.如图3所示.受水平拉力F作用.受地面摩擦力作用.两物体分别以加速度.运动.试确定F.与.的关系. 图3 分析:本题无须求与之间作用力的大小.可直接用牛顿第二定律在系统整体中应用. 点评:系统受到的合外力等于系统内各质点质量与其加速度乘积的矢量和. 练2:在粗糙的水平面上有一质量为M的三角形木块.两底角分别为..在三角形木块的两个粗糙斜面上.有两个质量为.的物体分别以.的加速度沿斜面下滑.三角形木块始终是相对地面静止.求三角形木块受到静摩擦力和支持力? 答案与提示:把..M看作一个系统.将加速度沿水平方向和竖直方向分解. 水平方向上: 竖直方向上: 解得:
网址:http://m.1010jiajiao.com/timu3_id_1535197[举报]
在“验证牛顿第二定律”的实验中,某实验小组设计了如下的实验方法. 如图所示,将导轨分上下双层水平排列,与两小车后部相连的刹车线穿过导轨尾端固定板,由安装在后面的刹车系统控制两小车同时起动和同时制动(图中未画).实验中可通过改变盘中的砝码来改变拉力的大小,通过放置在小车上的砝码个数改变小车的质量. 下表是该实验小组的实验数据,请根据实验要求将表中空格填上相应的数据和内容.
| 次 数 | 小 车 | 拉力 (N) | 质量 (g) | 位移 (cm) | 拉力 比值 (F甲:F乙) | 质量 比值 (m甲:m乙) | 位移 比值 (s甲:s乙) | 加速度 比值 (a甲:a乙) | 结论 |
| 1 | 甲 | 0.1 | 200 | 22.3 | 0.50 | 1 | |||
| 乙 | 0.2 | 200 | 43.5 | ||||||
| 2 | 甲 | 0.2 | 200 | 40.2 | 1 | 0.50 | |||
| 乙 | 0.2 | 400 | 19.5 |
在不改变实验装置的情况下,采用什么方法可减少实验误差(要求只说出一种你认为最重要的方法) ?
查看习题详情和答案>> 某同学为验证牛顿第二定律中“力与加速度”的关系,采用光电门系统来代替位移和时间测量工具,实验装置如图所示.光滑导轨水平放置,细线绕过可转动的圆形光栅连接小车与重物(重物质量远小于小车质量),挡板可以在小车到达的时候使小车停下并粘住.光电门在每次有红外线通过光栅时会记一次信号,如图所示,圆形光栅每转过一圈将会记下十次信号.不计一切摩擦,每次都将小车静止释放,在小车停止后,记下重物质量m、信号次数n、小车运动时间t.
某同学为验证牛顿第二定律中“力与加速度”的关系,采用光电门系统来代替位移和时间测量工具,实验装置如图所示.光滑导轨水平放置,细线绕过可转动的圆形光栅连接小车与重物(重物质量远小于小车质量),挡板可以在小车到达的时候使小车停下并粘住.光电门在每次有红外线通过光栅时会记一次信号,如图所示,圆形光栅每转过一圈将会记下十次信号.不计一切摩擦,每次都将小车静止释放,在小车停止后,记下重物质量m、信号次数n、小车运动时间t.
| 重物质量m | 信号次数n | 运动时间t(s) |
| m0 | 40 | 2.00 |
| 2m0 | 60 | 1.73 |
| 3m0 | 70 | t3 |
A、s∝n;B、s∝1/n;C、s∝n2;D、s∝1/n2
(2)若实验后得到了下表所示的数据,经分析可知,运动时间t3应为______s. 查看习题详情和答案>>
某同学为验证牛顿第二定律中“力与加速度”的关系,采用光电门系统来代替位移和时间测量工具,实验装置如图所示.光滑导轨水平放置,细线绕过可转动的圆形光栅连接小车与重物(重物质量远小于小车质量),挡板可以在小车到达的时候使小车停下并粘住.光电门在每次有红外线通过光栅时会记一次信号,如图所示,圆形光栅每转过一圈将会记下十次信号.不计一切摩擦,每次都将小车静止释放,在小车停止后,记下重物质量m、信号次数n、小车运动时间t.
(1)小车经过的位移s与光电门记下 的信号次数n的关系是______
A、s∝n;B、s∝1/n;C、s∝n2;D、s∝1/n2
(2)若实验后得到了下表所示的数据,经分析可知,运动时间t3应为______s.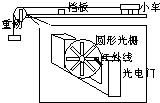
查看习题详情和答案>>
| 重物质量m | 信号次数n | 运动时间t(s) |
| m0 | 40 | 2.00 |
| 2m0 | 60 | 1.73 |
| 3m0 | 70 | t3 |
A、s∝n;B、s∝1/n;C、s∝n2;D、s∝1/n2
(2)若实验后得到了下表所示的数据,经分析可知,运动时间t3应为______s.

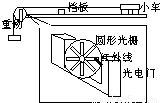
某同学为验证牛顿第二定律中“力与加速度”的关系,采用光电门系统来代替位移和时间测量工具,实验装置如图所示.光滑导轨水平放置,细线绕过可转动的圆形光栅连接小车与重物(重物质量远小于小车质量),挡板可以在小车到达的时候使小车停下并粘住.光电门在每次有红外线通过光栅时会记一次信号,如图所示,圆形光栅每转过一圈将会记下十次信号.不计一切摩擦,每次都将小车静止释放,在小车停止后,记下重物质量m、信号次数n、小车运动时间t.
(1)小车经过的位移s与光电门记下 的信号次数n的关系是______
A、s∝n;B、s∝1/n;C、s∝n2;D、s∝1/n2
(2)若实验后得到了下表所示的数据,经分析可知,运动时间t3应为______s.
 查看习题详情和答案>>
查看习题详情和答案>>
| 重物质量m | 信号次数n | 运动时间t(s) |
| m | 40 | 2.00 |
| 2m | 60 | 1.73 |
| 3m | 70 | t3 |
A、s∝n;B、s∝1/n;C、s∝n2;D、s∝1/n2
(2)若实验后得到了下表所示的数据,经分析可知,运动时间t3应为______s.
 查看习题详情和答案>>
查看习题详情和答案>>
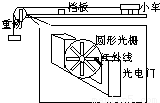
某同学为验证牛顿第二定律中“力与加速度”的关系,采用光电门系统来代替位移和时间测量工具,实验装置如图所示.光滑导轨水平放置,细线绕过可转动的圆形光栅连接小车与重物(重物质量远小于小车质量),挡板可以在小车到达的时候使小车停下并粘住.光电门在每次有红外线通过光栅时会记一次信号,如图所示,圆形光栅每转过一圈将会记下十次信号.不计一切摩擦,每次都将小车静止释放,在小车停止后,记下重物质量m、信号次数n、小车运动时间t.
(1)小车经过的位移s与光电门记下 的信号次数n的关系是______
A、s∝n;B、s∝1/n;C、s∝n2;D、s∝1/n2
(2)若实验后得到了下表所示的数据,经分析可知,运动时间t3应为______s.
 查看习题详情和答案>>
查看习题详情和答案>>
| 重物质量m | 信号次数n | 运动时间t(s) |
| m | 40 | 2.00 |
| 2m | 60 | 1.73 |
| 3m | 70 | t3 |
A、s∝n;B、s∝1/n;C、s∝n2;D、s∝1/n2
(2)若实验后得到了下表所示的数据,经分析可知,运动时间t3应为______s.
 查看习题详情和答案>>
查看习题详情和答案>>