如果乘客在地铁中能承受的最大加速度是1.4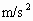，两相邻车站相距560m，则地铁列车在两站之间行驶的最短时间是________s，在上述条件下，列车行驶的最大速度为________m/s．

（20分）提高铁路运行时速是人们孜孜以求的。1966年，有人建议利用超导磁体和路基导体中的感应电流之间的磁力把列车悬浮起来运行，如图所示，在车辆底部安装超导磁体，在轨道两旁埋设一系列闭合的铝环。当列车运行时，超导磁体产生的磁场相对于铝环运动，列车凌空浮起，使车与轨道间的摩擦减少到零，如果要进一步减小运行中受到的空气阻力，可以使列车在抽成真空的地下隧道中行驶。由于阻力极小，车速可高达1000m/s。当然列车启动与停站均需有一个变速过程。设绝大多数乘客的生理能承受0.1g（g为重力加速度）的加速度。

   （1）分析使列车浮起的力的原因。

   （2）假设从东海之滨的上海到西域名城乌鲁木齐之间有这样的一条笔直的地下隧道。估计轨道的长度最接近于下列哪个数值？

A．500km   　B．1000km   C．4000km    D．8000km

   （3）乘坐超高速客车沿上述线路完成横跨祖国东西的漫长旅行最短时间是多少？

   （4）设列车的质量为5×10⁵kg，由于阻力极小，列车只需在加速阶段做功，而减速过程甚至可以利用特定装置回收列车释放的动能，把节省的能量用于产生真空，实现磁浮。试求上述运行每次可回收的能量。