网址:http://m.1010jiajiao.com/timu3_id_1530636[举报]
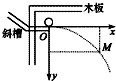 在“研究平抛物体的运动”的实验中:
在“研究平抛物体的运动”的实验中:(1)为使小球水平抛出,必须调整斜槽,使其末端的切线成水平方向,检查方法是
(2)小球抛出点的位置必须及时记录在白纸上,然后从这一点画水平线和竖直线作为x轴和y轴,竖直线是用
(3)验证实验得到的轨迹是否准确的一般方法是:在水平方向从起点处取两段连续相等的位移与曲线交于两点,作水平线交于y轴,两段y辆位移之比为
(4)某同学建立的直角坐标系如图所示,设他在安装实验装置和其余操作时准确无误,只有一处失误,即是
(5)该同学在轨迹上任取一点M,测得坐标为(x,y),则初速度的测量值为
|
|
|
|
 在“研究平抛物体的运动”的实验中:
在“研究平抛物体的运动”的实验中:(1)验证实验得到的轨迹是否准确的一般方法是:在水平方向从起点处取两段连续相等的位移交于曲线两点,作水平线交于y轴,两段y轴位移之比为
(2)某同学建立的直角坐标如图所示,设他在安装实验装置和其他操作时准确无误,只有一处失误,即
(3)该同学在轨迹上任取一点M,测得坐标为(x,y),初速度的测量值为
|
|
|
|
 在“研究平抛物体的运动”的实验中
在“研究平抛物体的运动”的实验中(1)为使小球水平抛出,必须调整斜槽,使其末端的切线成水平方向,检查方法是
(2)小球抛出点的位置必须及时记录在白纸上,然后从这一点面水平线和竖直线作为x轴和y轴,竖直线是用
(3)验证实验得到的轨迹是否准确的一般方法:在水平方向从起点处取两段连续相等的位移与曲线交于两点,作水平线交于y轴,两段y轴位移之比为
(1)为使小球水平抛出,必须调整斜槽,使其末端的切线成水平方向,检查方法是___________________________________________________________.
(2)小球抛出点的位置必须及时记录在白纸上,然后从这一点画水平线和竖直线作为x轴和y轴,竖直线是用___________来确定的.
(3)验证实验得到的轨迹是否准确的一般方法是:在水平方向从起点处取两段连续相等的位移与曲线交于两点,作水平线交于y轴,两段y辆位移之比为___________.
(4)某同学建立的直角坐标系如图所示,设他在安装实验装置和其余操作时准确无误,只有一处失误,即是_________________________________________________________________.
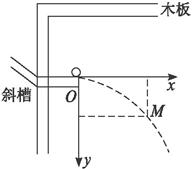
(5)该同学在轨迹上任取一点M,测得坐标为(x,y),则初速度的测量值为___________,真实值为___________.
查看习题详情和答案>>在“研究平抛物体的运动”的实验中:
(1)为使小球水平抛出,必须调整斜槽,使其末端的切线成水平方向,这样做的目的是_____________________________________。
(2)小球抛出点的位置必须及时记录在白纸上,然后从这一点画水平线和竖直线作为x轴和y轴,竖直线是用_________________来确定的。
(3)验证实验得到的轨迹是否准确的一般方法是:在水平方向从起点处取两段连续相等的位移与曲线交于两点,作水平线交于y轴,两段y轴位移之比为______________。
(4)某同学建立的直角坐标系如图所示,设他在安装实验装置和其余操作时准确无误,只有一处失误,即是_____________________________________________________________。
查看习题详情和答案>>