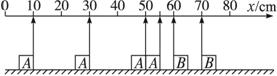
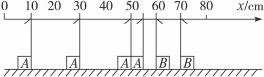
摘要:A.B两滑块在同一光滑的水平直导轨上相向运动发生碰撞.用闪光照相.闪光4次摄得的闪光照片如图5-15所示.已知闪光的时间间隔为Δt.而闪光本身持续时间极短.在这4次闪光的瞬间.A.B两滑块均在0-80 cm刻度范围内.且第一次闪光时.滑块A恰好通过x=55 cm处.滑块B恰好通过x=70 cm处.问: 图5-15 (1)碰撞发生在何处? (2)碰撞发生在第一次闪光后多长时间? (3)两滑块的质量之比等于多少? 解析:(1)据题意经分析可判定:碰撞发生在第1.2两次闪光时刻之间.碰撞后B静止.故碰撞发生在x=60 cm处. ① (2)碰撞后A向左做匀速运动.设其速度为vA′ vA′Δt=20 cm ② 从碰撞到第二次闪光时A向左运动10 cm.时间为.有:vA′=10 cm ③ 从第一次闪光到发生碰撞时间为t.有: t+=Δt ④ 由②③④可得:t=Δt/2. ⑤ (3)取向右为正方向 碰撞前:A的速度vA= ⑥ B的速度 vB=- ⑦ 碰撞后:A的速度vA′=- ⑧ B的速度vB′=0 ⑨ 由动量守恒定律.可得: mAvA+mBvB=mAvA′+mBvB′ ⑩ 由⑥⑦⑧⑨⑩可得:mA∶mB=2∶3. 答案:Δt/2 (3)2∶3
网址:http://m.1010jiajiao.com/timu3_id_1526718[举报]
 A、B两滑块在同一光滑的水平直导轨上相向运动发生碰撞(碰撞时间极短).用闪光照相,闪光4次摄得的闪光照片如图所示.已知闪光的时间间隔为△t,而闪光本身持续时间极短,在这4次闪光的瞬间,A、B两滑块均在0~80cm刻度范围内,且第一次闪光时,滑块A恰好通过x=55cm处,滑块B恰好通过x=70cm处,则
A、B两滑块在同一光滑的水平直导轨上相向运动发生碰撞(碰撞时间极短).用闪光照相,闪光4次摄得的闪光照片如图所示.已知闪光的时间间隔为△t,而闪光本身持续时间极短,在这4次闪光的瞬间,A、B两滑块均在0~80cm刻度范围内,且第一次闪光时,滑块A恰好通过x=55cm处,滑块B恰好通过x=70cm处,则(1)碰撞发生在x=
60cm
60cm
处(2)碰撞发生在第一次闪光后
| △t |
| 2 |
| △t |
| 2 |
(3)设两滑块的质量之比为mA:mB=2:3,试分析碰撞前后两滑块的质量与速度乘积之和是否相等?
是
是
(填“是”或者“不是”) A、B两滑块在同一光滑的水平直导轨上相向运动发生碰撞(碰撞时间及短),用闪光照相机,闪光4次摄得的闪光照片如图所示,已知闪光的时间间隔为△t,而闪光本身持续时间极短,在这4次闪光的瞬间,A、B两滑块均在0~80cm刻度范围内,且第一次闪光时,滑块A恰好通过x=55cm处,滑块B恰好通过x=70cm处,求:
A、B两滑块在同一光滑的水平直导轨上相向运动发生碰撞(碰撞时间及短),用闪光照相机,闪光4次摄得的闪光照片如图所示,已知闪光的时间间隔为△t,而闪光本身持续时间极短,在这4次闪光的瞬间,A、B两滑块均在0~80cm刻度范围内,且第一次闪光时,滑块A恰好通过x=55cm处,滑块B恰好通过x=70cm处,求:(1)碰撞发生在何处?
(2)碰撞发生在第一次闪光后多少时间?
A、B两滑块在同一光滑的水平直导轨上相向运动发生碰撞(碰撞时间极短).用闪光照相,闪光4次摄得的闪光照片如图16-1-7 所示.已知闪光的时间间隔为Δt,而闪光本身持续时间极短.在这4次闪光的瞬间,A、B两滑块均在0—80 cm 刻度范围内,且第一次闪光时,滑块A恰好通过x=55 cm 处,滑块B恰好通过x=70 cm 处.问:

图
(1)碰撞发生在何处?
(2)碰撞发生在第一次闪光后多长时间?
查看习题详情和答案>>