摘要:F2+ 根据机械能守恒定律可得 2lv12-v22 由图知F2=0.F1=Fm 由以上各式解得.反映系统性质的物理量是 m=-m0 l=g A.B一起运动过程中的守恒量是机械能E.若以最低点为零势能点.则 E=v12 解得E= g. ※[例5] 一个质量为M的雪橇静止在水平雪地上.一条质量为m的爱斯基摩狗站在该雪橇上.狗向雪橇的正后方跳下.随后又追赶并向前跳上雪橇,其后狗又反复地跳下.追赶并跳上雪橇.狗与雪橇始终沿一条直线运动.若狗跳离雪橇时雪橇的速度为V.则此时狗相对于地面的速度为V+u(其中u为狗相对于雪橇的速度.V+u为代数和.若以雪橇运动的方向为正方向.则V为正值.u为负值).设狗总以速度v追赶和跳上雪橇.雪橇与雪地间的摩擦忽略不计.已知v的大小为5 m/s.u的大小为4 m/s.M=30 kg.m=10 kg.求: (1)狗第一次跳上雪橇后两者的共同速度的大小, (2)雪橇最终速度的大小和狗最多能跳上雪橇的次数. (供使用但不一定用到的对数值:lg2=0.301.lg3=0.477) 解析:(1)设雪橇运动的方向为正方向.狗第1次跳下雪橇后雪橇的速度为V1.根据动量守恒定律.有MV1+m=0 狗第1次跳上雪橇时.雪橇与狗的共同速度v1′满足 MV1+mv=(M+m)V1′ 可解得V1′= 将u=-4 m/s.v=5 m/s.M=30 kg.m=10 kg代入.得V1′=2 m/s. (2)方法一:设雪橇运动的方向为正方向.狗第(n-1)次跳下雪橇后雪橇的速度为Vn-1.则狗第(n-1)次跳上雪橇后的速度Vn-1′满足MVn-1+mv=(M+m)Vn-1′ 这样.狗n次跳下雪橇后.雪橇的速度Vn满足MVn+mVn-1′ 解得Vn=n-1 狗追不上雪橇的条件是Vn≥v 可化为()n-1≤ 最后可求得 n≥1+ 代入数据.得n≥3.41 狗最多能跳上雪橇3次 雪橇最终的速度大小为V4=5.625 m/s. 方法二:设雪橇运动的方向为正方向.狗第i次跳下雪橇后.雪橇的速度为Vi.狗的速度为Vi+u,狗第i次跳上雪橇后.雪橇和狗的共同速度为Vi′.由动量守恒定律可得 第一次跳下雪橇:MV1+m=0 V1=-=1 m/s 第一次跳上雪橇:MV1+mv=(M+m)V1′ 第二次跳下雪橇: V2= 第三次跳下雪橇: V3′= 第四次跳下雪橇: V4==5.625 m/s 此时雪橇的速度已大于狗追赶的速度.狗将不可能追上雪橇.因此.狗最多能跳上雪橇3次.雪橇最终的速度大小为5.625 m/s. ●素质能力检测
网址:http://m.1010jiajiao.com/timu3_id_1526700[举报]
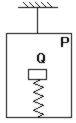
如图所示,吊篮P悬挂在天花板上,与吊篮质量相等的物体Q被固定在吊篮中的轻弹簧托起,当悬挂吊篮的细绳被剪断的瞬间,吊篮P和物体Q的加速度是:( )

A、g,g B、2g,g C、g,2g D、2g,0
查看习题详情和答案>>
 如图3-12-18所示,质量为m的小球用水平轻弹簧系住,并用倾角为30°的光滑木板AB托住,小球恰好处于静止状态.当木板AB突然向下撤离的瞬间,小球的加速度大小为 ( )
如图3-12-18所示,质量为m的小球用水平轻弹簧系住,并用倾角为30°的光滑木板AB托住,小球恰好处于静止状态.当木板AB突然向下撤离的瞬间,小球的加速度大小为 ( )
A.0 B.![]() C.g D.
C.g D.![]()
利用水滴下落可以测出重力加速度g,调节水龙头,让水一滴一滴地流出,在水龙头的正下方放一个盘子,调节盘子的高度,使一个水滴碰的盘子里恰好有一水滴从水龙头开始下落,而空中还有一个正在下落中的水滴.测出水龙头到盘子间距离为h(m),再用秒表测时间.以第一个水滴离开水龙头开始计时,到第N个水滴落至盘中,共计时间为T(s).
则:第一个水滴到盘子时,第二个水滴离开水龙头的距离是 m,
重力加速度g= m/s2。 查看习题详情和答案>>
则:第一个水滴到盘子时,第二个水滴离开水龙头的距离是 m,
重力加速度g= m/s2。 查看习题详情和答案>>
如图所示, 吊篮P悬挂在天花板上, 与吊篮质量相等的物体Q被固定在吊篮中的轻质弹簧托住, 当悬挂吊篮的细绳剪断的瞬间, 吊篮P和物体Q的加速度是
[ ]
| A.ap=g, aQ=g | B.ap=2g, aQ=g |
| C.ap=g, aQ=2g | D.ap=2g, aQ=0 |