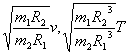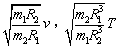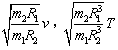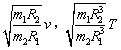摘要：设星球的质量为m1 月球的质量为m2 飞船的质量为m ,飞船距地球中心的距离为r 由万有引力定律公式 3 可知:G=G 4 又由 解得: r=54R 3 17．解:设抛出点的高度为h.第一次平抛的水平射程 为x.则有 x2+h2=L2 ① 2 由平抛运动规律得知.当初速增大到2倍.其水平 射程也增大到2x.可得 (2x)2+h2=(L)2 ② 2 由①.②解得 h=L/ 2 设该星球上的重力加速度为g.由平抛运动的规律. 得 h=gt2/2 2 由万有引力定律与牛顿第二定律.得 GMm/R2=mg 2 式中m为小球的质量.联立以上各式.解得 M=2LR2/(3Gt2) 2
网址：http://m.1010jiajiao.com/timu3_id_1525907[举报]
质量为m1的登月舱连接在质量为m2的轨道舱上一起绕月球作圆周运动，其轨道半径是月球半径Rm的3倍。某一时刻，登月舱与轨道舱分离，轨道舱仍在原轨轨道上运动，登月舱作一瞬间减速后，沿图示椭圆轨道登上月球表面，在月球表面逗留一段时间后，快速启动发动机，使登月舱具有一合适的初速度，使之沿原椭圆轨道回到脱离点与轨道舱实现对接。由开普勒第三定律可知，以太阳为焦点作椭圆轨道运行的所有行星，其椭圆轨道半长轴的立方与周期的平方之比是一个常量。另，设椭圆的半长轴为a，行星质量为m，太阳质量为M0，则行星的总能量为
。行星在椭圆轨道上运行时，行星的机械能守恒，当它距太阳的距离为r时，它的引力势能为
。G为引力恒量。设月球质量为M，不计地球及其它天体对登月舱和轨道舱的作用力。求：
（1）登月舱减速时，发动机做了多少功？
（2）登月舱在月球表面可逗留多长时间？
据悉，“嫦娥一号”月球探测卫星目前已完成方案设计和初样设计，各项专业试验正在进行，不久整星将转入正样研制阶段，计划2007年发射.按照目前的计划,“嫦娥一号”将从西昌卫星发射中心升空,首先进入周期为T1的近地圆轨道,然后在地面的指令下经过一系列的变轨后最终将停留在距离月球表面为h的月球极地轨道上绕月球做匀速圆周运动.已知地球质量为M1,半径为R1,月球质量为M2,半径为R2.求“嫦娥一号”绕月球运行时的周期T2.
查看习题详情和答案>>
设探月卫星“嫦娥1号”绕朋运行的轨道是圆形的，且贴近月球表面。已知月球的质量M2约为地球质量M1的
，月球的半径R2约为月球与地球距离R1的
，月球绕地球运动（看作圆周运动）的平均速率为v1=1.0km/s。“嫦娥1号”安装的太阳能电池帆板的面积S=8πm2。该太阳能电池将太阳能转化为电能的转化率η=11%。已知太阳光的总功率为P0=3.8×1026 W。月球与太阳之间的平均距离R=1.5×1011 m。估算（结果取2位有效数字）
（1）该探月卫星绕月运行的速率v2
（2）太阳光趋向太阳能电池帆板进太阳能电池的电功率P
查看习题详情和答案>>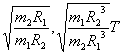
对应的环绕速度为T，则“嫦娥一号”环绕月球表面附近圆轨道飞行的速度和周期分别为
B．
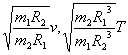
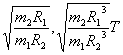D．
