摘要:例5.如图5所示.用一细线悬挂一根粗细均匀的轻质细麦桔杆.使其静止在水平方向上. O为麦桔杆的中点.这时有两只蚂蚁同时从O点分别向着麦桔杆的两端匀速爬行.在蚂蚁 爬行的过程中麦桔杆在水平方向始终保持乎衡.则( ) A.两蚂蚁的质量一定相等 B.两蚂蚁的爬行速度大小一定相等 C.两蚂蚁的质量与爬行速度大小的乘积一定相等 D.两蚂蚁对麦桔杆的压力一定相等 分析: 蚂蚁爬行的过程中麦桔杆始终保持乎衡.有.即.所以.故选C.
网址:http://m.1010jiajiao.com/timu3_id_1517765[举报]
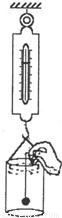
 如图所示,弹簧秤下悬挂一水桶,桶与水的总质量为5千克,用细线系一质量为1.78千克的实心铜球,用手提细线上端将小球缓慢浸没在水中,使铜球在水中静止不动,且不与桶壁、桶底接触,桶中的水也没有溢出.已知铜的密度为8.9×103千克/米3.试分析、计算在这种情况下,
如图所示,弹簧秤下悬挂一水桶,桶与水的总质量为5千克,用细线系一质量为1.78千克的实心铜球,用手提细线上端将小球缓慢浸没在水中,使铜球在水中静止不动,且不与桶壁、桶底接触,桶中的水也没有溢出.已知铜的密度为8.9×103千克/米3.试分析、计算在这种情况下,(1)铜球受到的浮力为多大?
(2)小球缓慢浸入水的过程中,水对桶底的压强是
(3)根据你的判断,小球缓慢浸入水的过程中,弹簧秤的示数将怎样变化?
 用一根细线把小钢球悬挂起来.这叫做单摆,是最简单的振动系统.如题图所示,将小球稍微拉离平衡位置到达a然后放手,它就开始摆动.假如没有空气阻力,小球将一直摆下去.永不停止.仔细观察摆动过程,可以发现小球来回摆动一次所需的时问总是一样的,这是单摆的等时性,这个时问称为振动的周期.小明猜想单摆周期的大小可能与单摆的摆长l、偏离中心位置的夹角θ及摆球的质量m有关.于是小明做了分别改变单摆的摆长、偏离中心位置的夹角、摆球的质量的摆动实验,并测出了各种情形下单摆的周期,如下表.
用一根细线把小钢球悬挂起来.这叫做单摆,是最简单的振动系统.如题图所示,将小球稍微拉离平衡位置到达a然后放手,它就开始摆动.假如没有空气阻力,小球将一直摆下去.永不停止.仔细观察摆动过程,可以发现小球来回摆动一次所需的时问总是一样的,这是单摆的等时性,这个时问称为振动的周期.小明猜想单摆周期的大小可能与单摆的摆长l、偏离中心位置的夹角θ及摆球的质量m有关.于是小明做了分别改变单摆的摆长、偏离中心位置的夹角、摆球的质量的摆动实验,并测出了各种情形下单摆的周期,如下表.表一 m=10g θ=4°
| 摆长/m | 0.5 | 1 | 1.5 | 2 |
| 周期/s | 1.4 | 2 | 2.4 | 2.8 |
| 摆角θ | 1° | 2° | 3° | 4° |
| 周期/s | 2 | 2 | 2 | 2 |
| 摆球质量/g | 5 | 10 | 15 | 20 |
| 周期/s | 2 | 2 | 2 | 2 |
单摆摆动周期与摆角和摆球质量无关,与摆长有关,摆长越长、摆动周期越大
单摆摆动周期与摆角和摆球质量无关,与摆长有关,摆长越长、摆动周期越大
.(2)单摆的等时性主要应用在
挂机械钟
挂机械钟
上.(3)机械摆钟走时太快,应将摆长
调长些
调长些
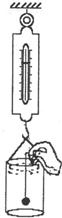
.如图所示,弹簧秤下悬挂一水桶,桶与水的总质量为5千克,用细线系一质量为1.78千克的实心铜球,用手提细线上端将小球缓慢浸没在水中,使铜球在水中静止不动,且不与桶壁、桶底接触,桶中的水也没有溢出。已知铜的密度为8.9×103千克/米3。试分析、计算在这种情况下,
(1)铜球受到的浮力为多大?
(2)小球缓慢浸入水的过程中,水对桶底的压强是________(选填“增大”、 “减小”或“不变”),这是因为_______________。
(3)根据你的判断,小球缓慢浸入水的过程中,弹簧秤的示数将怎样变化? ______________ (选填“增大”、“减小”或“不变”)
(1)铜球受到的浮力为多大?
(2)小球缓慢浸入水的过程中,水对桶底的压强是________(选填“增大”、 “减小”或“不变”),这是因为_______________。
(3)根据你的判断,小球缓慢浸入水的过程中,弹簧秤的示数将怎样变化? ______________ (选填“增大”、“减小”或“不变”)

用一根细线把小钢球悬挂起来.这叫做单摆,是最简单的振动系统.如题图所示,将小球稍微拉离平衡位置到达a然后放手,它就开始摆动.假如没有空气阻力,小球将一直摆下去.永不停止.仔细观察摆动过程,可以发现小球来回摆动一次所需的时问总是一样的,这是单摆的等时性,这个时问称为振动的周期.小明猜想单摆周期的大小可能与单摆的摆长l、偏离中心位置的夹角θ及摆球的质量m有关.于是小明做了分别改变单摆的摆长、偏离中心位置的夹角、摆球的质量的摆动实验,并测出了各种情形下单摆的周期,如下表.
表一 m=10g θ=4°
表二 m=10g l=1m
表三 θ=4° l=1m
(1)根据以上实验数据.分折得出的结论是______.
(2)单摆的等时性主要应用在______上.
(3)机械摆钟走时太快,应将摆长______.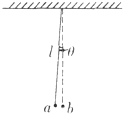
查看习题详情和答案>>
表一 m=10g θ=4°
| 摆长/m | 0.5 | 1 | 1.5 | 2 |
| 周期/s | 1.4 | 2 | 2.4 | 2.8 |
| 摆角θ | 1° | 2° | 3° | 4° |
| 周期/s | 2 | 2 | 2 | 2 |
| 摆球质量/g | 5 | 10 | 15 | 20 |
| 周期/s | 2 | 2 | 2 | 2 |
(2)单摆的等时性主要应用在______上.
(3)机械摆钟走时太快,应将摆长______.