摘要:26.如图所示是小明用来“探究串联电路中电压的规律 的实验装置及所用的电压表. ⑴ 请帮助小明设计一个用来记录电压值的表格.注明待测的电压值. ⑵ 这些电压之间的关系的表达式为 . ⑶ 在测灯L2两端的电压时.电压表的表笔1应接在 接线柱上.表笔2应接在 接线柱上.
网址:http://m.1010jiajiao.com/timu3_id_1508625[举报]
26、如图所示是小明用来“探究串联电路中电压的规律”的实验装置及所用的电压表.
(1)请帮助小明设计一个用来记录电压值的表格,注明待测的电压值(用字母表示).

(2)这些电压之间的关系的表达式为
(3)在测灯L2两端的电压时,电压表的表笔1应接在
查看习题详情和答案>>
(1)请帮助小明设计一个用来记录电压值的表格,注明待测的电压值(用字母表示).

(2)这些电压之间的关系的表达式为
UAD=UAB+UCD
.(3)在测灯L2两端的电压时,电压表的表笔1应接在
C(或B)
接线柱上,表笔2应接在D
接线柱上.(填上字母)
如图所示是小明用来“探究串联电路中电压的规律”的实验装置及所用的电压表.
(1)请帮助小明设计一个用来记录电压值的表格,注明待测的电压值(用字母表示).
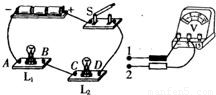
(2)这些电压之间的关系的表达式为______.
(3)在测灯L2两端的电压时,电压表的表笔1应接在______接线柱上,表笔2应接在______接线柱上.(填上字母)
查看习题详情和答案>>
(1)请帮助小明设计一个用来记录电压值的表格,注明待测的电压值(用字母表示).

(2)这些电压之间的关系的表达式为______.
(3)在测灯L2两端的电压时,电压表的表笔1应接在______接线柱上,表笔2应接在______接线柱上.(填上字母)
查看习题详情和答案>>
如图所示是小明用来“探究串联电路中电压的规律”的实验装置及所用的电压表。
(1)请帮助小明设计一个用来记录电压值的表格,注明待测的电压值(用字母表示)。
(2)这些电压之间的关系的表达式为_________________。
(3) 在测灯L2两端的电压时,电压表的表笔1应接在_________接线柱上,表笔2应接在__________接线柱上。(填上字母)
(1)请帮助小明设计一个用来记录电压值的表格,注明待测的电压值(用字母表示)。
(2)这些电压之间的关系的表达式为_________________。
(3) 在测灯L2两端的电压时,电压表的表笔1应接在_________接线柱上,表笔2应接在__________接线柱上。(填上字母)
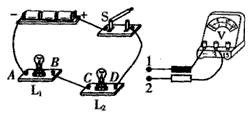
 如图所示是小明“探究串联电路中电压的关系”的实验电路图.
如图所示是小明“探究串联电路中电压的关系”的实验电路图.(1)实验步骤(请完成步骤中所缺内容)
A.按图所示接好电路,闭合开关前,滑片P应置于
右
右
端.B.滑片P移到适当位置,用电压表测出定值电阻R0两端的电压U1.
C.
保持滑片P不动,用电压表测出灯泡L两端的电压U2
保持滑片P不动,用电压表测出灯泡L两端的电压U2
.D.保持滑片P不动,用电压表测出a、b两点之间的电压U.
E.移动滑片P的位置,重复步骤B、C、D两次.
(2)讨论交流
小明通过对实验数据分析,得到结论:串联电路中各个电阻两端的电压相等,总电压等于各个电阻两端电压之和.
另一小组的小芳通过实验得到结论:串联电路中各个电阻两端的电压不相等,总电压等于各个电阻两端电压之和.
你认为
小芳
小芳
的结论更合理.理由是小明所用定值电阻的阻值与灯泡的阻值相同,而小芳的不同.
小明所用定值电阻的阻值与灯泡的阻值相同,而小芳的不同.
.(3)小明按图所示接好电路,闭合开关S,无论怎样移动滑片P,灯泡都不亮,但电压表有读数,经检查:除灯L和定值电阻R0外,其余都没有问题,则电路中存在的故障可能是
灯泡L短路或R0断路
灯泡L短路或R0断路
.为进一步确定故障,接下来的操作是(可以不受器材的限制)电压表接在滑动变阻器R两端并观察电压表有无示数
电压表接在滑动变阻器R两端并观察电压表有无示数
.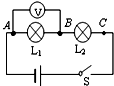 如图所示是小明“探究串联电路中电压的关系”的实验电路图.
如图所示是小明“探究串联电路中电压的关系”的实验电路图.【实验步骤】
1)将电源、两个规格相同的灯泡用导线按图所示的电路图
连接起来;
2)闭合开关,用电压表测出L1两端的电压;
3)在测L2两端的电压时,小明同学为了节省实验时间,采用以下方法:电压表所接的B接点不动,只断开A接点,并改接到C接点上;
4)测出AC间的电压.
【讨论交流】
(1)小明同学用上面的方法能否测出L2两端的电压?为什么?
不能,电压表的指针会反向偏转
不能,电压表的指针会反向偏转
.| UAB/V | UBC/V | UAC/V |
| 1.4 | 1.4 | 2.8 |
L1断路
L1断路
.(3)排除故障并改进方法后,小明所测出AB、BC、AC间的电压记录在右面表格中.并由此得到结论:串联电路中各个电阻两端的电压相等,总电压等于各个电阻两端电压之和.本实验设计存在不合理或可以改进的地方,请你指出:a
所用灯泡规格相同,具有特殊性
所用灯泡规格相同,具有特殊性
b
实验次数太少存在偶然性
实验次数太少存在偶然性
.