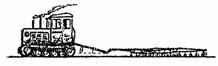
摘要:11.如图5-1-22所示.质量为M的拖拉机拉着耙来耙地.由静止开 始做匀加速直线运动.在时间t内前进的距离为x.耙地时.拖拉机受到的牵引力恒为F. 受到地面的阻力为自重的k倍.耙所受阻力恒定.连接杆质量不计且与水平面的夹角θ 保持不变.求: 图5-1-22 (1)拖拉机的加速度大小. (2)拖拉机对连接杆的拉力大小. (3)时间t内拖拉机对耙做的功. 解析:(1)由匀变速直线运动的公式:x=at2① 得:a=② (2)设连接杆对拖拉机的拉力为f.由牛顿第二定律得: F-kMg-fcos θ=Ma③ 根据牛顿第三定律.联立②③式.解得拖拉机对连接杆的拉力大小为: f′=f=④ (3)拖拉机对耙做的功: W=f′xcos θ⑤ 联立④⑤式.解得: W=x⑥ 答案: (3)x
网址:http://m.1010jiajiao.com/timu3_id_1392964[举报]
(2010·四川理综)质量为M的拖拉机拉着耙来耙地,由静止开始做匀加速直线运动,在时间t内前进的距离为x.耙地时,拖拉机受到的牵引力恒为F,受到地面的阻力为自重的k倍,耙所受阻力恒定,连接杆质量不计且与水平面的夹角θ保持不变.求:
(1)拖拉机的加速度大小.
(2)拖拉机对连接杆的拉力大小.
(3)时间t内拖拉机对耙做的功.
(2010·四川理综卷·15)下列说法正确的是 ( )
A.α粒子大角度散射表明α粒子很难进入原子内部
B.氢原子跃迁发出的光从空气射入水时可能发生全反射
C.裂变反应有质量亏损,质量数不守恒
D.γ射线是一种波长很短的电磁波
查看习题详情和答案>>
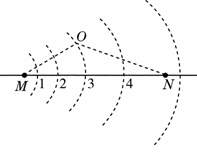
(2010·四川理综)如图所示,圆弧虚线表示正点电荷电场的等势面,相邻两等势面间的电势差相等.光滑绝缘直杆沿电场方向水平放置并固定不动,杆上套有一带正电的小滑块(可视为质点),滑块通过绝缘轻弹簧与固定点O相连,并以某一初速度从M点运动到N点,OM<ON.若滑块在M、N时弹簧的弹力大小相等,弹簧始终在弹性限度内,则( )
A.滑块从M到N的过程中,速度可能一直增大
B.滑块从位置1到2的过程中,电场力做的功比从位置3到4的小
C.在M、N之间的范围内,可能存在滑块速度相同的两个位置
D.在M、N之间可能存在只由电场力确定滑块加速度大小的三个位置