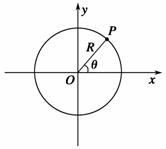
摘要： 如图10-1-26所示.一小型发电机内有n＝100匝的矩形线圈. 线圈面积S＝0.10 m2.线圈电阻可忽略不计．在外力作用下矩形线 圈在B＝0.10 T的匀强磁场中.以恒定的角速度ω＝100π rad/s绕垂 直于磁场方向的固定轴OO′匀速转动.发电机线圈两端与R＝100 Ω 的电阻构成闭合回路．求: (1)线圈转动时产生感应电动势的最大值, (2)从线圈平面通过中性面时开始.线圈转过90°角的过程中通过电阻R横截面的电荷量, (3)线圈匀速转动10 s.电流通过电阻R产生的焦耳热． 解析:(1)线圈中感应电动势的最大值Em＝nBSω＝3.14×102 V. (2)设从线圈平面通过中性面时开始.线圈转过90°角所用时间为Δt.线圈中的平均感应电动势＝n 通过电阻R的平均电流＝＝ 在Δt时间内通过电阻横截面的电荷量 Q＝Δt＝＝1.0×10-2 C. (3)矩形线圈在匀强磁场中匀速转动产生正弦交变电流.电阻两端电压的有效值U＝ Em经过t＝10 s电流通过电阻产生的焦耳热Q热＝t 解得Q热＝4.9×103 J. 答案:(1)3.14×102 V (2)1.0×10-2 C (3)4.9×103 J
网址：http://m.1010jiajiao.com/timu3_id_1392923[举报]
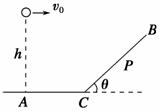
如图5－1－26所示，一个小球从高h＝10 m处以水平速度v0＝10 m/s抛出，撞在倾角θ＝45 °的斜面上的P点，已知AC＝5 m(g＝10 m/s2)，求：
(1)P、C之间的距离．
(2)小球撞击P点时速度的大小和方向．
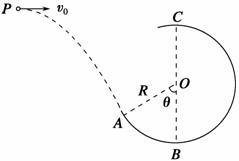
如图5－2－26所示，一个质量为0.6 kg的小球以某一初速度从P点水平抛出，恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力，进入圆弧时无机械能损失)．已知圆弧的半径R＝0.3 m，θ＝60°，小球到达A点时的速度vA＝4 m/s.(取g＝10 m/s2)求：
(1)小球做平抛运动的初速度v0；
(2)P点与A点的水平距离和竖直高度；
(3)小球到达圆弧最高点C时对轨道的压力．
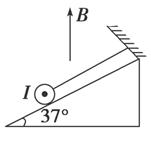
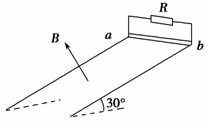
如图9－3－26所示，电阻可忽略的光滑平行金属导轨长s＝1.15 m，两导轨间距L＝0.75 m，导轨倾角为30°，导轨上端ab接一阻值R＝1.5 Ω 的电阻，磁感应强度B＝0.8 T的匀强磁场垂直轨道平面向上．阻值r＝0.5 Ω，质量m＝0.2 kg的金属棒与轨道垂直且接触良好，从轨道上端ab处由静止开始下滑至底端，在此过程中金属棒产生的焦耳热Q1＝0.1 J．(取g＝10 m/s2)求：
(1)金属棒在此过程中克服安培力的功W安；
(2)金属棒下滑速度v＝2 m/s时的加速度a.
(3)为求金属棒下滑的最大速度vm，有同学解答如下：由动能定理，W重－W安＝
mv
，…….由此所得结果是否正确？若正确，说明理由并完成本小题；若不正确，给出正确的解答．
