网址:http://m.1010jiajiao.com/timu3_id_1390977[举报]
(11分)(2009·北京模拟)在坐标系xOy中,有三个靠在一起的等大的圆形区域,分别存在着方向如图所示的匀强磁场,磁感应强度大小都为B=0.10T,磁场区域半径r=m,三个圆心A、B、C构成一个等边三角形,B、C点都在x轴上,且y轴与圆形区域C相切,圆形区域A内磁场垂直纸面向里,圆形区域B、C内磁场垂直纸面向外.在直角坐标系的第Ⅰ、Ⅳ象限内分布着场强E=1.0×105N/C的竖直方向的匀强电场,现有质量m=3.2×10-26kg,带电荷量q=-1.6×10-19C的某种负离子,从圆形磁场区域A的左侧边缘以水平速度v=106m/s沿正对圆心A的方向垂直磁场射入,求:
(1)该离子通过磁场区域所用的时间.
(2)离子离开磁场区域的出射点偏离最初入射方向的侧移为多大?(侧移指垂直初速度方向上移动的距离)
(3)若在匀强电场区域内竖直放置一挡板MN,欲使离子打到挡板MN上的偏离最初入射方向的侧移为零,则挡板MN应放在何处?匀强电场的方向如何?
查看习题详情和答案>>
(11分)(2009·广东高考)为了清理堵塞河道的冰凌,空军实施投弹爆破.飞机在河道上空高H处以速度v0水平匀速飞行,投掷下炸弹并击中目标.求炸弹刚脱离飞机到击中目标所飞行的水平距离及击中目标时的速度大小.(不计空气阻力)
查看习题详情和答案>>
(11分)(2009·安徽省六校联考)如图所示,为某种新型设备内部电、磁场分布情况图.自上而下分为Ⅰ、Ⅱ、Ⅲ三个区域.区域Ⅰ宽度为d1,分布有沿纸面向下的匀强电场E1;区域Ⅱ宽度为d2,分布有垂直纸面向里的匀强磁场B1;宽度可调的区域Ⅲ中分布有沿纸面向下的匀强电场E2和垂直纸面向里的匀强磁场B2.现在有一群质量和带电荷量均不同的带正电粒子从区域Ⅰ上边缘的注入孔A点被注入,从静止开始运动,然后相继进入Ⅱ、Ⅲ两个区域,满足一定条件的粒子将回到区域Ⅰ,其他粒子则从区域Ⅲ飞出.三区域都足够长,粒子的重力不计.
已知能飞回区域Ⅰ的带电粒子的质量为m=6.4×10-27kg,带电荷量为q=3.2×10-19C,且d1=10cm,d2=5cm,d3>10cm,E1=E2=40V/m,B1=4×10-3T,B2=2×10-3T.
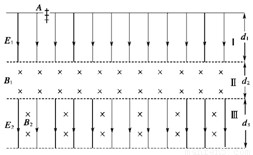
试求:
(1)该带电粒子离开区域Ⅰ时的速度.
(2)该带电粒子离开区域Ⅱ时的速度.
(3)该带电粒子第一次回到区域Ⅰ的上边缘时离开A点的距离.
查看习题详情和答案>>
(11分)(2009·安徽省六校联考)如图所示,为某种新型设备内部电、磁场分布情况图.自上而下分为Ⅰ、Ⅱ、Ⅲ三个区域.区域Ⅰ宽度为d1,分布有沿纸面向下的匀强电场E1;区域Ⅱ宽度为d2,分布有垂直纸面向里的匀强磁场B1;宽度可调的区域Ⅲ中分布有沿纸面向下的匀强电场E2和垂直纸面向里的匀强磁场B2.现在有一群质量和带电荷量均不同的带正电粒子从区域Ⅰ上边缘的注入孔A点被注入,从静止开始运动,然后相继进入Ⅱ、Ⅲ两个区域,满足一定条件的粒子将回到区域Ⅰ,其他粒子则从区域Ⅲ飞出.三区域都足够长,粒子的重力不计.
已知能飞回区域Ⅰ的带电粒子的质量为m=6.4×10-27kg,带电荷量为q=3.2×10-19C,且d1=10cm,d2=5cm,d3>10cm,E1=E2=40V/m,B1=4×10-3T,B2=2×10-3T.
试求:
(1)该带电粒子离开区域Ⅰ时的速度.
(2)该带电粒子离开区域Ⅱ时的速度.
(3)该带电粒子第一次回到区域Ⅰ的上边缘时离开A点的距离.
查看习题详情和答案>>
(11分)(2009·安徽省六校联考)如图所示,为某种新型设备内部电、磁场分布情况图.自上而下分为Ⅰ、Ⅱ、Ⅲ三个区域.区域Ⅰ宽度为d1,分布有沿纸面向下的匀强电场E1;区域Ⅱ宽度为d2,分布有垂直纸面向里的匀强磁场B1;宽度可调的区域Ⅲ中分布有沿纸面向下的匀强电场E2和垂直纸面向里的匀强磁场B2.现在有一群质量和带电荷量均不同的带正电粒子从区域Ⅰ上边缘的注入孔A点被注入,从静止开始运动,然后相继进入Ⅱ、Ⅲ两个区域,满足一定条件的粒子将回到区域Ⅰ,其他粒子则从区域Ⅲ飞出.三区域都足够长,粒子的重力不计.
已知能飞回区域Ⅰ的带电粒子的质量为m=6.4×10-27kg,带电荷量为q=3.2×10-19C,且d1=10cm,d2=5cm,d3>10cm,E1=E2=40V/m,B1=4×10-3T,B2=2×10-3T.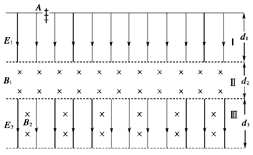
试求:
(1)该带电粒子离开区域Ⅰ时的速度.
(2)该带电粒子离开区域Ⅱ时的速度.
(3)该带电粒子第一次回到区域Ⅰ的上边缘时离开A点的距离.