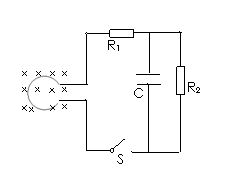
摘要：15．截面积S＝0.2m2.匝数n＝100匝的线圈A.处在如图(甲)所示的磁场中.磁感应强度B随时间按图(乙)所示规律变化.方向垂直线圈平面.规定向外为正方向．电路中R1＝4Ω.R2＝6Ω.C＝30μF.线圈电阻不计． (1)闭合S稳定后.求通过R2的电流, (2)闭合S一段时间后再断开.则断开后通过R2的电荷量是多少? [解析] 由于线圈A所在的磁场变化引起穿过线圈的磁通量发生变化.产生感应电动势．当S闭合后.就有电流通过R1.R2. (1)由图知B随时间按线性变化.变化率＝0.2T/s.由法拉第电磁感应定律得E＝nS＝4V.由楞次定律确定电流方向.在0-1s内.原磁场为负.即向里.大小在减小.故感应电流的磁场方向与原磁场方向相同.因此由安培定则知线圈中的电流方向为顺时针方向．从电路角度来看.线圈就是电源.其内阻不计.R1和R2串联后构成外电路.C与R2并联.当电流恒定时.电容器支路中无电流．由闭合电路欧姆定律得流过R2的电流I＝＝0.4A.方向向下． (2)S闭合后.将对C充电.充电结束后电容器支路断路.电容器两端的电势差等于R2两端的电压．因此.其充电量Q＝CU＝CE＝7.2×10-5C.S断开后.电容器通过R2放电.所以放电量为7.2×10-5C. [答案] 7.2×10-5C
网址：http://m.1010jiajiao.com/timu3_id_1390706[举报]
（12分）横截面积S＝0.2m2、n＝100匝的圆形线圈A处在如图所示的匀强磁场中，磁感应强度变化率为0.02T/s，开始时S未闭合，R1＝4Ω，R2＝6Ω，C＝30μF，线圈电阻不计，求：
（1）闭合S后，通过R2的电流的大小；
（2）闭合S后一段时间又断开，问S断开后通过R2的电荷量是多少？
 |
查看习题详情和答案>>
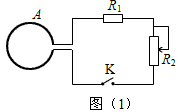
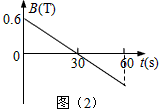
如图（1）所示，截面积S＝0.2m2，n＝100匝的圆形线圈A处在磁场中，磁场方向与线圈平面垂直，磁感应强度B随时间t变化的图象如图（2）所示，t＝0时刻，电键K闭合。已知R1＝4W，滑动变阻器R2的最大电阻为6W，线圈内阻不计，在滑动片移动的过程中，线圈A中的感应电流的最大值为___________A，滑动变阻器R2的最大功率为________________W。
如图所示，导热良好的薄壁气缸放在光滑水平面上，用横截面积为S＝1.0×10－2m2的光滑薄活塞将一定质量的理想气体封闭在气缸内，活塞杆的另一端固定在墙上．外界大气压强p0＝1.0×105Pa。当环境温度为27℃时，密闭气体的体积为2.0×10－3m3。
①当环境温度缓慢升高到87℃时，气缸移动了多少距离？
②如果环境温度保持在87℃，对气缸施加水平作用力，使缸内气体体积缓慢地恢复到原来数值，这时气缸受到的水平作用力多大？
＝0．02
的规律均匀减小，开始时S未闭合。R1＝4Ω，R2=6Ω，C=30µF，线圈内阻不计。求：
