摘要:12.如图所示.电容为C.带电荷量为Q.极板间距为d的电容器固定在绝缘底座上.两板竖直放置.总质量为m.整个装置静止在光滑水平面上.在电容器右板上有一小孔.一质量为m0.带电荷量为+q的弹丸以速度v0从小孔水平射入电容器中(不计弹丸重力.设电容器周围电场强度为0).弹丸最远可到达距右板为x(x<d)的P点.求: (1)弹丸在电容器中受到的电场力的大小, (2)x的值, (3)电容器获得的最大速度. 分析:x是相对位移.该位移乘以电场力等于电势能的增量.同时也等于机械能的减少量.弹丸最终返回从右板小孔飞出时.电容器速度最大.而不是弹丸与电容器速度相等时.电容器速度最大. 解析:(1)电容器两极板间电压U=① 极板间场强E=② 由①②式得F=qE=③ (2)弹丸到达P点时两者有共同速度.设为v.由动量守恒有:m0v0=(m0+m)v④ 对弹丸.由功能关系得:Fx=m0v-(m0+m)v2⑤ 由③④⑤式解得x=⑥ (3)弹丸最终返回从右板小孔飞出.此时电容器速度最大.设电容器速度为v1.弹丸速度为v2. 则由动量守恒有:m0v0=mv1-m0v2⑦ 在整个过程中由能量守恒.即 m0v=mv+m0v⑧ 由⑦⑧两式解得v1=
网址:http://m.1010jiajiao.com/timu3_id_1390419[举报]
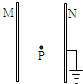 如图所示,电容量为C的平行板电容器的两极板M、N带有等量异种电荷,其中的N板接地.已知一电子(电荷量为-e)从远处运动到两板间中点P的过程中,电势能增加了E,则由此可推知M极板的带电情况为( )
如图所示,电容量为C的平行板电容器的两极板M、N带有等量异种电荷,其中的N板接地.已知一电子(电荷量为-e)从远处运动到两板间中点P的过程中,电势能增加了E,则由此可推知M极板的带电情况为( )A、带正电,电荷量为
| ||
B、带负电,电荷量为
| ||
C、带正电,电荷量为
| ||
D、带负电,电荷量为
|
 如图所示,电压U保持恒定,C1、C2是两个不同的电容器,且C1>C2,R1、R2、R3为不同阻值的电阻.开始时,C1与C2所带电荷量相等,如果把C1与R1对换位置,其他条件不变.下列判断错误的是( )
如图所示,电压U保持恒定,C1、C2是两个不同的电容器,且C1>C2,R1、R2、R3为不同阻值的电阻.开始时,C1与C2所带电荷量相等,如果把C1与R1对换位置,其他条件不变.下列判断错误的是( )
查看习题详情和答案>>
 如图所示,电流表、电压表均为理想电表,L为小电珠,R为滑动变阻器,电源电动势为E,内阻为r.现将开关S闭合,当滑动变阻器滑片P向左移动时,下列结论正确的是( )
如图所示,电流表、电压表均为理想电表,L为小电珠,R为滑动变阻器,电源电动势为E,内阻为r.现将开关S闭合,当滑动变阻器滑片P向左移动时,下列结论正确的是( )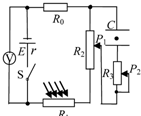 如图所示,电源电动势为E,内阻为r.电路中的R2、R3分别为总阻值一定的滑动变阻器,R0为定值电阻,R1为光敏电阻(其电阻随光照强度增大而减小).当电键S闭合时,电容器中一带电微粒恰好处于静止状态.有关下列说法中正确的是( )
如图所示,电源电动势为E,内阻为r.电路中的R2、R3分别为总阻值一定的滑动变阻器,R0为定值电阻,R1为光敏电阻(其电阻随光照强度增大而减小).当电键S闭合时,电容器中一带电微粒恰好处于静止状态.有关下列说法中正确的是( )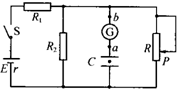 如图所示,电源电动势为E,内阻为r,平行板电容器C的两金属板水平放置.G为灵敏电流计.开关S闭合后,两板间恰好有一质量为m、电荷量为q的油滴处于静止状态.则在滑动变阻器R的触头P向上移动的过程中,下列判断正确的是( )
如图所示,电源电动势为E,内阻为r,平行板电容器C的两金属板水平放置.G为灵敏电流计.开关S闭合后,两板间恰好有一质量为m、电荷量为q的油滴处于静止状态.则在滑动变阻器R的触头P向上移动的过程中,下列判断正确的是( )