网址:http://m.1010jiajiao.com/timu3_id_1386951[举报]
(2010·潍坊质检)压敏电阻的阻值会随所受压力的增大而减小.一同学利用压敏电阻设计了判断升降机运动状态的装置,如图1甲所示,将压敏电阻平放在升降机内,受压面朝上,在上面放一物体m,升降机静止时电流表示数为I0.某过程中电流表的示数如图乙所示,则在此过程中 ( )
A.物体处于失重状态
B.物体处于超重状态
C.升降机一定向上做匀加速运动
D.升降机可能向下做匀减速运动
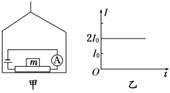
图1
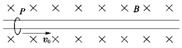
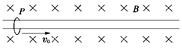
查看习题详情和答案>>(2010·潍坊)如图所示,质量为m,带电荷量为+q的P环套在固定的水平长直绝缘杆上,整个装置处在垂直于杆的水平匀强磁场中,磁感应强度大小为B.现给环一向右的初速度v0,则 ( )
A.环将向右减速,最后匀速
B.环将向右减速,最后停止运动
C.从环开始运动到最后达到稳定状态,损失的机械能是mv
D.从环开始运动到最后达到稳定状态,损失的机械能是mv-m2
查看习题详情和答案>>
(4分)(2010·潍坊质检)某同学利用如图7所示的两种装置探究平抛运动,方案如下:
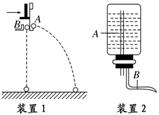
图7
装置1:用小锤打击金属片,A球水平抛出,同时B球自由下落.仔细观察A、B两球是否同时落到水平地面上.若同时落地,则说明水平分运动是匀速运动,竖直分运动是自由落体运动.
装置2:竖直管A上端要高于水面,这样可在较长时间内得到稳定的细水柱.水平管B喷出水流,在紧靠水流、平行于水流的玻璃板上用彩笔描出水流的轨迹,这就是平抛运动的轨迹.
找出以上叙述中不当之处并写到下面:
(1)__ ____________________________________________________________________;
(2)______________________________________________________________________.
查看习题详情和答案>>