摘要:12.如图所示.半径为R的半球支撑面顶部有一小孔.质量分别为m1和m2的两只小球.通过一根穿过半球顶部小孔的细线相连.不计所有摩擦.请你分析: (1)m2小球静止在球面上时.其平衡位置与半球面的球心连线跟水平方向的夹角为θ.则m1.m2.θ和R之间应满足什么关系, (2)若m2小球静止于θ=45°处.现将其沿半球面稍稍向下移动一些.则释放后m2能否回到原来位置? [答案] (1)m1=m2cosθ与R无关 (2)不能 [解析] (1)根据平衡条件有m2gcosθ=m1g.所以m1=m2cosθ(或cosθ=).与R无关. (2)不能回到原来位置.m2所受的合力为m2gcosθ′-m1g=m2g(cosθ′-cos45°)>0(因为θ′<45°).所以m2将向下运动.
网址:http://m.1010jiajiao.com/timu3_id_1386908[举报]
如图所示,半径为R的半球支撑面顶部有一小孔,质量分别为m1和m2的两只小球(视为质点),通过一根穿过半球顶部小孔的细线相连,不计所有摩擦,请你分析
(1)m2小球静止在球面上时,其平衡位置与半球面的球心连线跟水平方向的夹角为θ,则m1、m2,θ和R之间应满足什么关系;
(2)若m2小球静止于θ=45°处,现将其沿半球面稍稍向下移动一些,则释放后m2能否回到原来位置?请作简析。
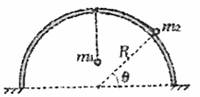
如图所示,半径为R的半球支撑面顶部有一小孔. 质量分别为m1和m2的两只小球(视为质点),通过一根穿过半球顶部小孔的细线相连,不计所有摩擦. 请你分析
小题1:m2小球静止在球面上时,其平衡位置与半球面的球心连线跟水平方向的夹角为θ,则m1、m2、θ和R之间应满足什么关系;
小题2:若m2小球静止于θ=45°处,现将其沿半球面稍稍向下移动一些,则释放后m2能否回到原来位置?请作简析。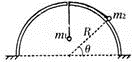
小题1:m2小球静止在球面上时,其平衡位置与半球面的球心连线跟水平方向的夹角为θ,则m1、m2、θ和R之间应满足什么关系;
小题2:若m2小球静止于θ=45°处,现将其沿半球面稍稍向下移动一些,则释放后m2能否回到原来位置?请作简析。

如图所示http://www.ks5u.com,半径为R的半球支撑面顶部有一小孔. 质量分别为m1和m2的两只小球(视为质点),通过一根穿过半球顶部小孔的细线www.ks5u.com相连,不计所有摩擦. 请你分析
m2小球静止在球面上时,其平衡位置与半球面的球心连线跟水平方向的夹角为θ,则m1、m2、θ和R之间应满足什么关系;
若m2小球静止于θ=45°处,现将其沿半球面稍稍向下移动一些,则释放后m2能否回到原来位置?请作简析。

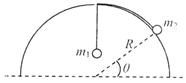
(2012年5月山东省烟台二模)如图所示,半径为R的半球支撑面顶部有一小孔,质量分别为m1和m2的两个小球(视为质点),通过一根穿过半球顶部小孔的细线相连,不计所有的摩擦,当小球m2静止在球面上、其平衡位置与半球面的球心连线跟水平面的夹角为θ时,则m1、m2,、θ之间的关系为
A. m1=m2sinθ
B.m1=m2/sinθ
C.m1=m2cosθ
D.m1=m2/cosθ
查看习题详情和答案>>
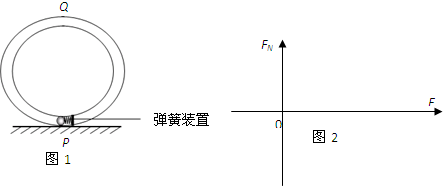
在电视中我们常看见魔术师使圆筒在空中无任何支撑条件下运动,简称“魔环运动”,其原理如图1所示.即水平地面上竖直放置一个质量为m、半径为R的光滑金属圆筒,在圆筒最底点P安装一个储备一定能量的弹簧装置,将一质量为2m的小球A(可视为质点)置于P点,打开弹簧装置将弹簧储备的能量全部转移给A,A就会从圆筒的P点运动到最高点Q,又从Q点运动P点,在这一过程中,圆筒将离开地面时而向上或向下运动,这就是“魔环运动”.设筒的内径、弹簧装置的大小、圆筒自身的运动可以忽略,完成下列问题:
(1)要使A要到达Q点,求A在P点的最小速度.
(2)当A运动到Q点时,要使圆筒离开地面,求A在Q点的最小速度.
(3)当A运动到Q点时,要使圆筒具有大小为g,方向竖直向上的加速,则弹射装置应该储备的能量?
(4)以A在最高点对圆筒的作用力FN为纵坐标(规定向上为正),弹簧装置储备的能量E为横坐标,在图2中作出FN-E图象.
查看习题详情和答案>>
(1)要使A要到达Q点,求A在P点的最小速度.
(2)当A运动到Q点时,要使圆筒离开地面,求A在Q点的最小速度.
(3)当A运动到Q点时,要使圆筒具有大小为g,方向竖直向上的加速,则弹射装置应该储备的能量?
(4)以A在最高点对圆筒的作用力FN为纵坐标(规定向上为正),弹簧装置储备的能量E为横坐标,在图2中作出FN-E图象.
