摘要: 如右图所示.某货场需将质量为m1=100 kg的货物从高处运送至地面.为避免货物与地面发生撞击.现利用固定于地面的光滑四分之一圆轨道.使货物由轨道顶端无初速滑下.轨道半径R=1.8 m.地面上紧靠轨道依次排放两块完全相同的木板A.B.长度均为l=2 m.质量均为m2=100 kg.木板上表面与轨道末端相切.货物与木板间的动摩擦因数为μ1.木板与地面间的动摩擦因数μ2=0.2.(最大静摩擦力与滑动摩擦力大小相等.取g=10 m/s2) (1)求货物到达圆轨道末端时对轨道的压力. (2)若货物滑上木板A时.木板不动.而滑上木板B时.木板B开始滑动.求μ1应满足的条件. (3)若μ1=0.5.求货物滑到木板A末端时的速度和在木板A上运动的时间. [解析] (1)设货物滑到轨道末端时的速度为v0.对货物的下滑过程.根据机械能守恒定律得 m1gR=m1v① 设货物在轨道末端所受支持力的大小为FN.根据牛顿第二定律得 FN-m1g=m1② 联立①②式.代入数据得 FN=3 000 N③ 根据牛顿第三定律.货物对轨道的压力大小为3 000 N.方向竖直向下. (2)若滑上木板A上时.木板不动.由受力分析得 μ1m1g≤μ2(m1+2m2)g④ 若滑上木板B时.木板B开始滑动.由受力分析得 μ1m1g>μ2(m1+m2)g⑤ 联立④⑤式.代入数据得
网址:http://m.1010jiajiao.com/timu3_id_1385983[举报]
(2009年高考广东卷)硅光电池是利用光电效应原理制成的器件,下列表述正确的是( )
A.硅光电池是把光能转变为电能的一种装置
B.硅光电池中吸收了光子能量的电子都能逸出
C.逸出的光电子的最大初动能与入射光的频率无关
D.任意频率的光照射到硅光电池上都能产生光电效应
查看习题详情和答案>>
(2009年高考福建理综卷改编)如图9-3-14所示,固定放置在同一水平面内的两根平行长直金属导轨的间距为d,其右端接有阻值为R的电阻,整个装置处在竖直向上磁感应强度大小为B的匀强磁场中.一质量为m(质量分布均匀)的导体杆ab垂直于导轨放置,且与两导轨保持良好接触,杆与导轨之间的动摩擦因数为μ.现杆在水平向左、垂直于杆的恒力F作用下从静止开始沿导轨运动距离l时,速度恰好达到最大(运动过程中杆始终与导轨保持垂直).设杆接入电路的电阻为r,导轨电阻不计,重力加速度大小为g.则此过程( )

图9-3-14
A.杆的速度最大值为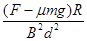
B.流过电阻R的电量为
C.恒力F做的功与摩擦力做的功之和等于杆动能的变化量
D.恒力F做的功与安培力做的功之和等于杆动能的变化量
查看习题详情和答案>>
(2009年高考辽宁、宁夏理综卷)关于光电效应,下列说法正确的是( )
A.极限频率越大的金属材料逸出功越大
B.只要光照射的时间足够长,任何金属都能产生光电效应
C.从金属表面出来的光电子的最大初动能越大,这种金属的逸出功越小
D.入射光的光强一定时,频率越高,单位时间内逸出的光电子数就越多
查看习题详情和答案>>
