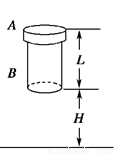
摘要：13．如图所示.一个厚度不计的圆环A.紧套在长度为L的圆柱体B的上端.A.B两者的质量均为m.A与B之间的最大静摩擦力与滑动摩擦力相同.其大小为kmg(k>1)．B在离地H高处由静止开始落下.触地后能竖直向上弹起.触地时间极短.且无动能损失.B与地碰撞若干次后A与B分离．求: (1)B与地第一次碰撞后.经多长时间A与B达到相同的速度, (2)当A与B第一次达到相同速度时.B下端离地面的高度是多少． [答案] H [解析] (1)B与地第一次碰撞后.以v0＝向上运动.加速度aB＝(k+1)g.方向向下, 此时刻A以速度v0＝向下运动.加速度aA＝(k-1)g.方向向上． 取向下为正方向.设A.B共同速度为v1. 对A有:v1＝v0-(k-1)gt. 对B有:v1＝-v0+(k+1)gt 解得t＝ (2)由以上各式解得.A与B第一次达到的相同速度v1＝.方向向下． 解法一 B下端离地面的高度h＝v0t-＝H. 解法二 用平均速度求解:h＝t＝H. 解法三 用动能定理:对B.-(mg+kmg)h＝mv-mv.解得h＝H.
网址：http://m.1010jiajiao.com/timu3_id_1382246[举报]
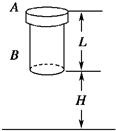如图所示，一个厚度不计的圆环A，紧套在长度为L的圆柱体B的上端，A、B两者的质量均为m，A与B之间的最大静摩擦力与滑动摩擦力相同，其大小为kmg（k＞1）．B在离地H高处由静止开始落下，触地后能竖直向上弹起，触地时间极短，且无动能损失，B与地碰撞若干次后A与B分离．求：（1）B与地第一次碰撞后，经多长时间A与B达到相同的速度；
（2）当A与B第一次达到相同速度时，B下端离地面的高度是多少．
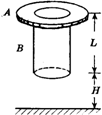如图所示，一个厚度不计的圆环A，紧套在长度为L的圆柱体B的上端，A、B两者的质量均为m．A与B之间的最大静摩擦力与滑动摩擦力相同，其大小为kmg（k＞1）．B由离地H高处由静止开始落下，触地后能竖直向上弹起，触地时间极短，且无动能损失．（l）B与地第一次碰撞后，B上升的最大高度是多少？
（2）B与地第一次碰撞后，当A与B刚相对静止时，B下端离地面的高度是多少？
（3）要使A、B不分离，L至少应为多少？
（12分）如图所示，一个厚度不计的圆环A，紧套在长度为L的圆柱体B的上端，A、B两者的质量均为m，A与 B之间的最大静摩擦力与滑动摩擦力相同，其大小为kmg（k>1）。B在离地H高处由静止开始落下，触地后能竖直向上弹起，触地时间极短，且无动能损失，B与地碰撞若干次后A与B分离。求：
（1）B与地第一次碰撞后，经多长时间A与B达到相同的速度；
（2）当A与B第一次达到相同速度时，B下端离地面的高度。
查看习题详情和答案>>
