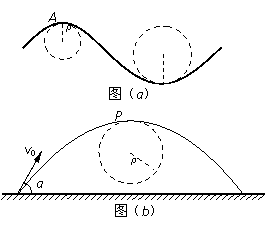
摘要：一般的曲线运动:在一般的曲线运动中仍有法向力式中R为研究处曲线的曲率半径.即在该处附近取一段无限小的曲线.并视为圆弧.R为该圆弧的曲率半径.即为研究处曲线的曲率半径. [典型例题] 例题1:如图所示.以水平初速度抛出的物体.飞行一段时间后.垂直地撞在倾角为的斜面上.求物体完成这段飞行的时间是多少? 例题2:如果把上题作这样的改动:若让小球从斜面顶端A以水平速度抛出.飞行一段时间后落在斜面上的B点.求它的飞行时间为多少(已知)? 例题3:斜向上抛出一球.抛射角,当t=1秒钟时.球仍斜向上升.但方向已跟水平成角.(1)球的初速度是多少?(2)球将在什么时候达到最高点? 例题4:以v0=10m/s的初速度自楼顶平抛一小球.若不计空气阻力.当小球沿曲线运动的法向加速度大小为5m/s时.求小球下降的高度及所在处轨迹的曲率半径R.
网址：http://m.1010jiajiao.com/timu3_id_1377905[举报]
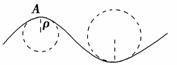
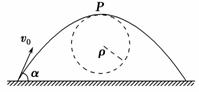
一般的曲线运动可以分成很多小段，每小段都可以看成圆周运动的一部分，即把整条曲线用一系列不同半径的小圆弧来代替．如图甲所示，曲线上A点的曲率圆定义为：在曲线上某一点A和邻近的另外两点分别做一圆，当邻近的另外两点无限接近A点时，此圆的极限位置叫做曲线A点处的曲率圆，其曲率圆半径R叫做A点的曲率半径．现将一质量为m的物体沿与水平面成θ角的方向以某一速度抛出，如图乙所示．不计空气阻力，在其轨迹最高点P处的曲率半径为r，则（ ）
一般的曲线运动可以分成很多小段，每小段用不同半径的小圆弧来代替．通过曲线上某点作曲率圆，其半径是该点的曲率半径．现将一物体在竖直平面内沿与水平方向成一定角度从A点抛出，最高点B点的曲率半径为ρ，线OBM竖直，落地时轨迹与ON相切于C点，且∠MON=θ，不计空气阻力，重力加速度为g，如图所示．求：（1）物体抛出时的初速度；
（2）O点与B点的高度差．
一般的曲线运动可以分成很多小段，每小段都可以看成圆周运动的一部分，即把整条曲线用一系列不同半径的小圆弧来代替，如图（a）所示，曲线上的A点的曲率圆定义为：通过A点和曲线上紧邻A点两侧的两点作一圆．在极限情况下，这个圆就叫做A点的曲率圆，其半径ρ叫做A点的曲率半径．现将一物体沿与水平面成α角的方向以速度v0抛出，如图（b）所示，则在其轨迹最高点P处的曲率半径是（ ）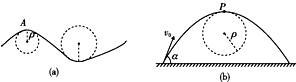
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
B．
D．
B.
C.
D.