摘要:两个天体间存在万有引力.并具有由相对位置决定的势能.如果两个天体的质量分别为m1和m2.当它们相距无穷远时势能为零.则它们的距离为r时.引力势能Ep=-G.发射地球同步卫星时.一般是把它先送入较低的圆形轨道.如图所示.再经过两次点火.即先在图中a点处启动燃气发动机.向后喷出高压燃气.卫星得到加速.进入图中的椭圆轨道Ⅱ,在轨道Ⅱ的远地点b处第二次点火.卫星再次被加速.此后.卫星沿图中的圆形轨道Ⅲ运动.设某同步卫星的质量为m.地球半径为R.轨道Ⅰ距地面非常近.轨道Ⅲ距地面的距离近似为6R.地面处的重力加速度为g.并且每次点火经历的时间都很短.点火过程中卫星减少的质量可以忽略. (1)从轨道Ⅰ转移到轨道Ⅲ的过程中.合力对卫星所做的总功是多大? (2)若已知卫星在轨道Ⅱ上经过a点时的速率为.则在b处点火的过程中燃气对卫星所做的功是多少? 解析:(1)卫星在轨道Ⅰ和轨道Ⅲ做圆周运动.应满足: G=m.G=m 得:Ek1=mv=G=mgR Ek3=mv=mgR 合力做的功W=Ek3-Ek1=mgR(-)=-mgR. (2)卫星在a处的势能Ep1=G=-mgR 卫星在b处的势能Ep2=G=-mgR 卫星在轨道Ⅱ上经过b处的速度为vb.由机械能守恒定律有: Epa+Eka=Epb+Ekb 解得:Ekb=mv=mgR 故在a处燃气所做的功W=Ek3-Ekb=mgR. 答案:(1)-mgR (2)mgR
网址:http://m.1010jiajiao.com/timu3_id_1376384[举报]
两个天体(包括人造天体)间存在万有引力,并具有由相对位置决定的热能。如果两个天体的质量分别为m1和m2,当它们相距无穷远时势能为零,则它们距离为r时,引力势能为EP=-G。
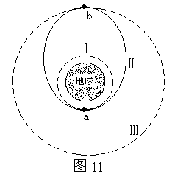
发射地球同步卫星一般是把它先送入较低的圆形轨道,如图11中Ⅰ,再经过两次“点火”,即先在图中a点处启动燃气发动机,向后喷出高压燃气,卫星得到加速,进入图11中的椭圆轨道Ⅱ,在轨道Ⅱ的远地点b处第二次“点火”,卫星再次被加速,此后,沿图中的圆形轨道Ⅲ(即同步轨道)运动。
设某同步卫星的质量为m,地球半径为R,轨道Ⅰ距地面非常近,轨道Ⅲ距地面的距离近似为6R,地面处的重力加速度为g,并且每次点火经历的时间都很短,点火过程中卫星的质量减少可以忽略。求:(1)从轨道Ⅰ转移到轨道Ⅲ的过程中,合力对卫星所做的总功是多大?(2)两次“点火”过程中燃气对卫星所做的总功是多少?
 查看习题详情和答案>>
查看习题详情和答案>>
发射地球同步卫星一般是把它先送入较低的圆形轨道,如图11中Ⅰ,再经过两次“点火”,即先在图中a点处启动燃气发动机,向后喷出高压燃气,卫星得到加速,进入图11中的椭圆轨道Ⅱ,在轨道Ⅱ的远地点b处第二次“点火”,卫星再次被加速,此后,沿图中的圆形轨道Ⅲ(即同步轨道)运动。
设某同步卫星的质量为m,地球半径为R,轨道Ⅰ距地面非常近,轨道Ⅲ距地面的距离近似为6R,地面处的重力加速度为g,并且每次点火经历的时间都很短,点火过程中卫星的质量减少可以忽略。求:(1)从轨道Ⅰ转移到轨道Ⅲ的过程中,合力对卫星所做的总功是多大?(2)两次“点火”过程中燃气对卫星所做的总功是多少?
 查看习题详情和答案>>
查看习题详情和答案>>