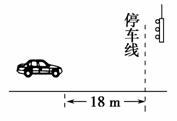
4．图5-3-18 如图5-3-18所示.静止放在水平桌面上的纸带.其上有一质量为m＝0.1 kg的铁块.它与纸带右端的距离为L＝0.5 m.铁块与纸带间.纸带与桌面间动摩擦因数均为μ＝0.——青夏教育精英家教网—

摘要：4．图5-3-18 如图5-3-18所示.静止放在水平桌面上的纸带.其上有一质量为m＝0.1 kg的铁块.它与纸带右端的距离为L＝0.5 m.铁块与纸带间.纸带与桌面间动摩擦因数均为μ＝0.1.现用力F水平向左将纸带从铁块下抽出.当纸带全部抽出时铁块恰好到达桌面边缘.铁块抛出后落地点离抛出点的水平距离为s＝0.8 m．已知g＝10 m/s2.桌面高度为H＝0.8 m.不计纸带质量.不计铁块大小.铁块不滚动．求: (1)铁块抛出时速度大小, (2)纸带从铁块下抽出所用时间t1, (3)纸带抽出过程产生的内能E. 解析:(1)水平方向:s＝vt① 竖直方向:H＝gt2② 由①②联立解得:v＝2 m/s. (2)设铁块的加速度为a1.由牛顿第二定律.得μmg＝ma1③ 纸带抽出时.铁块的速度v＝a1t1④ ③④联立解得t1＝2 s. (3)铁块的位移s1＝a1t⑤ 设纸带的位移为s2,由题意知.s2-s1＝L⑥ 由功能关系可得E＝μmgs2+μmg(s2-s1)⑦ 由③④⑤⑥⑦联立解得E＝0.3 J. 答案:0.3 J

网址：http://m.1010jiajiao.com/timu3_id_1374952[举报]

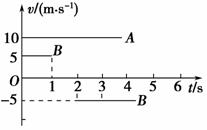
如图1－3－18所示，是A、B两质点运动的速度图像，则下列说法错误的是 (　　)．

A．A质点以10 m/s的速度匀速运动

B．B质点先以5 m/s的速度与A同方向运动1 s，而后停了1 s，最后以5 m/s相反方向的速度匀速运动

C．B质点最初3 s内的位移是10 m

D．B质点最初3 s内的路程是10 m

查看习题详情和答案>>

如图5－1－18所示，船从A处开出后沿直线AB到达对岸，若AB与河岸成37°角，水流速度为4 m/s，则船从A点开出的最小速度为 (　　)．

A．2 m/s B．2.4 m/s

C．3 m/s D．3.5 m/s

查看习题详情和答案>>

如图4－4－18所示，一质量m＝0.4 kg的滑块(可视为质点)静止于动摩擦因数μ＝0.1的水平轨道上的A点．现对滑块施加一水平外力，使其向右运动，外力的功率恒为P＝10.0 W．经过一段时间后撤去外力，滑块继续滑行至B点后水平飞出，恰好在C点沿切线方向进入固定在竖直平面内的光滑圆弧形轨道，轨道的最低点D处装有压力传感器，当滑块到达传感器上方时，传感器的示数为25.6 N．已知轨道AB的长度L＝2.0 m，半径OC和竖直方向的夹角α＝37°，圆形轨道的半径R＝0.5 m．(空气阻力可忽略，重力加速度g＝10 m/s²，sin 37°＝0.6，cos 37°＝0.8)，求：