网址：http://m.1010jiajiao.com/timu3_id_1374844[举报]
某同学设计了一个探究加速度a与物体所受合力F及质量m关系的实验，图4－2－13甲为实验装置简图(交流电的频率为50 Hz)．
图4－2－13
(1)图乙为某次实验得到的纸带，根据纸带可求出小车的加速度大小为________m/s2(保留两位有效数字)．
(2)保持砂和砂桶质量不变，改变小车质量m，分别得到小车加速度a与质量m及对应的
，数据如下表：
| 实验次数 物理量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 小车加速度a/(m·s－2) | 1.90 | 1.72 | 1.49 | 1.25 | 1.00 | 0.75 | 0.50 | 0.30 |
| 小车质量m/kg | 0.25 | 0.29 | 0.33 | 0.40 | 0.50 | 0.71 | 1.00 | 1.67 |
|
| 4.00 | 3.45 | 3.03 | 2.50 | 2.00 | 1.41 | 1.00 | 0.60 |
请在如图4－2－14所示的方格坐标纸中画出a－图线，并依据图线求出小车加速度a与质量倒数之间的关系式是________．
图4－2－14
图4－2－15
(3)保持小车质量不变，改变砂和砂桶质量，该同学根据实验数据作出了加速度a随合力F的变化图线，如图4－2－15所示．该图线不通过原点，请你分析其主要原因是________________________________________________________________________
________________________________________________________________________.
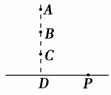
查看习题详情和答案>>如图4－2－15所示，P是水平地面上的一点，A、B、C、D在一条竖直线上，且AB＝BC＝CD.从A、B、C三点分别水平抛出一个物体，这三个物体都落在水平地面上的P点．则三个物体抛出时速度大小之比vA∶vB∶vC为 ( )．
A.
∶
∶
B．1∶∶
C．1∶2∶3 D．1∶1∶1
如图4－2－15所示，一块长木板B放在光滑的水平面上，再在B上放一物体A，现以恒定的外力拉B，A、B发生相对滑动，向前移动了一段距离．在此过程中 ( )．
A．B对A的摩擦力所做的功等于A的动能增加量
B．A对B的摩擦力所做的功等于B对A的摩擦力所做的功
C．外力F做的功等于A和B动能的增加量
D．外力F对B做的功等于B的动能的增加量与B克服摩擦力所做的功之和
