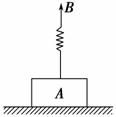
摘要： 图4-4-11 欧盟和我国合作的“伽利略 全球卫星定位系统的空间部分由平均分布在三个轨道平面上的30颗轨道卫星构成.每个轨道平面上有10颗卫星.从而实现高精度的导航定位．现假设“伽利略 系统中每颗卫星均围绕地心O做匀速圆周运动.轨道半径为r.一个轨道平面上某时刻10颗卫星所在位置如图4-4-11所示.相邻卫星之间的距离相等.卫星1和卫星3分别位于轨道上A.B两位置.卫星按顺时针运行．地球表面重力加速度为g.地球的半径为R.不计卫星间的相互作用力．求卫星1由A位置运行到B位置所需要的时间． 解析:设地球质量为M.卫星质量为m.每颗卫星的运行周期为T.万有引力常量为G.由万有引力定律和牛顿定律有G＝mr2 ① 地球表面重力加速度为g＝G ② 联立①②式可得T＝ ③ 卫星1由A位置运行到B位置所需要的时间为t＝T ④ 联立③④式可得t＝ . 答案: () 来源: 版权所有:() 版权所有:() 版权所有:()
网址：http://m.1010jiajiao.com/timu3_id_1374639[举报]
如图4－11所示，细线的一端固定于倾角为45°的光滑楔形滑块A的顶端P处，细线的另一端拴一质量为m的小球．当细线对小球的拉力刚好等于零时，水平向右的加速度a的大小为(g为重力加速度)( )
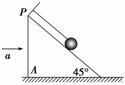
图4－11
A．g B．2g
C.
g D.
g
某同学在做测定电源的电动势和内电阻的实验中，用同一套器材采用如图4-3-11 中甲、乙所示的两种不同电路进行测量，并在同一坐标系中作出了两次测定的U-I图线如图4-3-11中丙所示，图中的C点与A点很接近，试问：
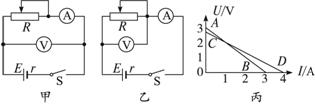
图
（1）图线AB是按哪种电路的测量作出的?
（2）电池的电动势、内电阻的真实值是多少?
（3）电流表的内阻是多少?
查看习题详情和答案>>用落体法“验证机械能守恒定律”的实验中：(g取9.8 m/s2)
(1)运用公式
mv2＝mgh时对实验条件的要求是________________．为此目的，所选择的纸带第1、2两点间的距离应接近__________．
(2)若实验中所用重物质量m＝1 kg，打点纸带如图实－4－10所示，打点时间间隔为0.02 s，则记录B点时，重物速度vB＝________，重物动能Ek＝________；从开始下落起至B点，重物的重力势能减小量是__________，由此可得出的结论是____________________________________．
图实－4－10
(3)根据纸带算出各点的速度v，量出下落距离h，则以
为纵轴，以h为横轴画出的图象应是图实－4－11中的
( )
图实－4－11
查看习题详情和答案>>
