如图5－2－18所示，斜轨道与半径为R的半圆轨道平滑连接，点A与半圆轨道最高点C等高，B为轨道的最低点．现让小滑块(可视为质点)从A点开始以速度v₀沿斜面向下运动，不计一切摩擦，关于滑块运动情况的分析，正确的是                     (　　)．

A．若v₀＝0，小滑块恰能通过C点，且离开C点后做自由落体运动

B．若v₀＝0，小滑块恰能通过C点，且离开C点后做平抛运动

C．若v₀＝，小滑块恰能到达C点，且离开C点后做自由落体运动

D．若v₀＝，小滑块恰能到达C点，且离开C点后做平抛运动

如图5－1－18所示，船从A处开出后沿直线AB到达对岸，若AB与河岸成37°角，水流速度为4 m/s，则船从A点开出的最小速度为     (　　)．

A．2 m/s                  B．2.4 m/s

C．3 m/s                  D．3.5 m/s

如图4－2－18所示，理想变压器原线圈中正弦式交变电源的输入电压和电流分别为U₁和I₁，两个副线圈的输出电压和电流分别为U₂和I₂、U₃和I₃，接在原、副线圈中的五个完全相同的灯泡均正常发光，则下列关系中正确的是(　　)

图4－2－18

A．I₁∶I₂∶I₃＝1∶2∶1

B．U₁∶U₂∶U₃＝1∶1∶2

C．三个线圈匝数之比为n₁∶n₂∶n₃＝5∶2∶1

D．电源电压U₁与原线圈两端电压U之比为1∶1

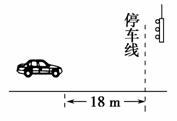
如图1－2－3所示，以8 m/s匀速行驶的汽车即将通过路口，绿灯还有2 s就熄灭，此时汽车距离停车线18 m．该车加速时最大加速度大小为2 m/s²，减速时最大加速度大小为5 m/s².此路段允许行驶的最大速度为12.5 m/s.下列说法中正确的有　　　　　　　 (　　)．

A．如果立即以最大加速度做匀加速运动，在绿灯熄灭前汽车可能通过停车线

B．如果立即以最大加速度做匀加速运动，在绿灯熄灭前通过停车线汽车一定超速

C．如果立即以最大加速度做匀减速运动，在绿灯熄灭前汽车一定不能通过停车线

D．如果距停车线5 m处以最大加速度减速，汽车能停在停车线处

如图4－4－18所示，一质量m＝0.4 kg的滑块(可视为质点)静止于动摩擦因数μ＝0.1的水平轨道上的A点．现对滑块施加一水平外力，使其向右运动，外力的功率恒为P＝10.0 W．经过一段时间后撤去外力，滑块继续滑行至B点后水平飞出，恰好在C点沿切线方向进入固定在竖直平面内的光滑圆弧形轨道，轨道的最低点D处装有压力传感器，当滑块到达传感器上方时，传感器的示数为25.6 N．已知轨道AB的长度L＝2.0 m，半径OC和竖直方向的夹角α＝37°，圆形轨道的半径R＝0.5 m．(空气阻力可忽略，重力加速度g＝10 m/s²，sin 37°＝0.6，cos 37°＝0.8)，求：

 (1)滑块运动到C点时速度v_C的大小；

(2)B\，C两点的高度差h及水平距离x；

(3)水平外力作用在滑块上的时间t.

图4－4－18